KosmologÐa. BasileÐou S. Gerogiˆnnh. Kajhght Tm matoc Fusik c PanepisthmÐou Patr n
|
|
|
- Ἀπολλωνία Φραγκούδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 KosmologÐa BasileÐou S. Gerogiˆnnh Kajhght Tm matoc Fusik c PanepisthmÐou Patr n Patra 2016
2 Kefˆlaio 1 Eisagwgikˆ 1.1 Gwniakì mègejoc, parsèk, ètoc fwtìc Ο παρατηρητής του Σχήματος 1.1 παρατηρεί από απόσταση d ένα αντικείμενο γραμμικού μεγέθους D. Η γωνία α υπό την οποία βλέπει το αντικείμενο ο παρατηρητής ονομάζεται «γωνιακό μέγεθος» ή «γωνιακή διάμετρος» του αντικειμένου. Το γωνιακό μέγεθος α εξαρτάται από την απόσταση d ενώ το γραμμικό μέγεθος D του αντικειμένου είναι, προϕανώς, ανεξάρτητο της απόστασης. Σχήμα 1.1: Γραμμικό και γωνιακό μέγεθος αντικειμένου. Από το Σχήμα 1.1 συνάγεται ότι D/2 d ( α ) = tan. (1.1) 2 Στην περίπτωση των αστρονομικών παρατηρήσεων, τα γωνιακά μεγέθη είναι μικρές γωνίες. Γνωρίζουμε από την τριγωνομετρία ότι η εϕαπτομένη μίας μικρής γωνίας, α 2, είναι προσεγγιστικά ίση με την ίδια τη γωνία εκϕρασμένη σε ακτίνια (radians, rads), tan( α 2 ) α 2. Συνεπώς, η Εξίσωση 1.1 γράϕεται D = α d. (1.2) Στην πράξη, τα γωνιακά μεγέθη των ουράνιων σωμάτων μετριούνται σε «δευτερόλεπτα τόξου» (arcseconds, arcsec). Ο συντελεστής μετατροπής των arcsec σε rads μπορεί να υπολογισθεί με την απλή μέθοδο (αϕού 2π rads = arcsec), 1 arcsec 1 rads. (1.3)
3 1.2 Κινητική θεωρία της θερμότητας 2 Άν λοιπόν το γωνιακό μέγεθος, α, έχει μετρηθεί σε arcsec, τότε η Εξίσωση 1.2 γράϕεται D = α d (1.4) Για έναν παρατηρητή ευρισκόμενο σε μεγάλη απόσταση από το Ηλιακό Σύστημα, το γωνιακό μέγεθος της ακτίνας της τροχιάς της Γης περί τον Ηλιο, ϖ, ονομάζεται «παράλλαξη». Ο παρατηρητής μπορεί να προσδιορίσει την απόστασή του από τον Ηλιο θέτοντας στην Εξίσωση 1.4 α = ϖ για το γωνιακό μέγεθος σε arcsec, D = a E για το γραμμικό μέγεθος, και λύνοντας ως προς d, d = a E. (1.5) ϖ Το σύμβολο a E παριστάνει τη μέση ακτίνα της τροχιάς της Γης περί τον Ηλιο, η οποία αναϕέρεται ως «αστρονομική μονάδα» (Astronomical Unit, AU), 1 AU = a E km. (1.6) Άν υποθέσουμε ότι ο παρατηρητής βρίσκεται τόσο μακρυά, ώστε να έχει παράλλαξη ϖ = 1 arcsec, τότε η απόστασή του από τον Ηλιο είναι d = AU. Η απόσταση αυτή χρησιμοποιείται στην αστροϕυσική ως μονάδα μέτρησης αποστάσεων και ονομάζεται «παρσέκ» (parsec, pc), 1 pc = AU km. (1.7) Το «έτος ϕωτός» (light year, ly) είναι μία ακόμη μονάδα μέτρησης αποστάσεων, πολύ χρήσιμη στην αστροϕυσική. Ορίζεται ως η απόσταση που διανύει σε ευθεία γραμμή ένα ϕωτόνιο κινούμενο με ταχύτητα c = m s 1 επί ένα έτος, 1 ly = c = m = AU. (1.8) Από τις Εξισώσεις 1.7 και 1.8 προκύπτει ότι 1 pc = 3.26 ly. (1.9) 1.2 'Ennoiec apì thn kinhtik jewrða thc jermìthtac Η κινητική θεωρία της θερμότητας εδράζεται στην υπόθεση ότι η εσωτερική ενέργεια ενός σώματος λόγω της θερμικής κίνησης των συστατικών σωματίων του (ατόμων ή μορίων) είναι ανάλογη της απόλυτης θερμοκρασίας του σώματος. Εϕαρμογή της θεωρίας αυτής στα αέρια αποϕέρει την κινητική θεωρία των ιδανικών αερίων, η οποία στηρίζεται στις ακόλουθες υποθέσεις. 1. Τα σωμάτια ενός ιδανικού αερίου κινούνται ως υλικά σϕαιρίδια άτακτα και προς όλες τις διευθύνσεις, έτσι ώστε σε κάθε χρονική στιγμή να κινείται ίδιος αριθμός σωματίων προς κάθε διεύθυνση. 2. Τα σωμάτια ασκούν δυνάμεις μόνο κατά τη στιγμή της σύγκρουσής τους με άλλα σωμάτια ή με τα τοιχώματα του δοχείου που περιέχει το ιδανικό αέριο. Συνεπώς, μεταξύ δύο διαδοχικών συγκρούσεών του, ένα σωμάτιο κινείται ευθύγραμμα και ομαλά. 3. Οι συγκρούσεις των σωματίων, μεταξύ τους ή με τα τοιχώματα του δοχείου,
4 1.3 Εννοιες από τη ϕυσική του ϕωτός 3 θεωρούνται ελαστικές, οπότε η ολική κινητική ενέργεια του ιδανικού αερίου παραμένει σταθερή επομένως σταθερή παραμένει και η θερμοκρασία του αερίου. 4. Ο συνολικός όγκος των σωματίων θεωρείται αμελητέος σε σύγκριση με τον όγκο του δοχείου που περιέχει το ιδανικό αέριο. Ενα σημαντικό συμπέρασμα της θεωρίας αυτής είναι ότι οι ταχύτητες των συστατικών σωματίων ενός ιδανικού αερίου δεν έχουν ούτε το ίδιο μέτρο, ούτε την ίδια διεύθυνση. Ενα μικρό ποσοστό των σωματίων έχει πολύ μικρές ή πολύ μεγάλες ταχύτητες όμως το μεγαλύτερο ποσοστό έχει ενδιάμεσες ταχύτητες. Προκύπτει έτσι η κατανομή ταχυτήτων κατά Maxwell Boltzmann. Η μέση κινητική ενέργεια ενός σωματίου, ϵ, το οποίο εκτελεί μόνο μεταϕορική κίνηση, είναι ίση με ( ) mv 2 ϵ = 3 k T 2 2, (1.10) όπου m είναι η μάζα του συστατικού σωματίου και T η απόλυτη θερμοκρασία του ιδανικού αερίου. Η Εξίσωση 1.10 επιλύεται ως προς τη «μέση ταχύτητα», v, και δίνει 3 k T v = m. (1.11) Η σταθερά k των Εξισώσεων ονομάζεται «σταθερα του Boltzmann» και έχει την τιμή k = J K 1 (1.12) Ακριβέστεροι υπολογισμοί αποϕέρουν έναν ελαϕρώς διαϕορετικό αριθμητικό όρο στην Εξίσωση 1.11 συγκεκριμένα, ο όρος 3 αντικαθίσταται από τον όρο 8 π, 8 k T v = π m. (1.13) Άν η μέση ταχύτητα των συστατικών σωματίων ενός αερίου είναι μεγαλύτερη του ενός έκτου της ταχύτητας διαϕυγής ενός πλανήτη, v > 1 6 v,planet, τότε το αέριο διαϕεύγει προοδευτικά και η ατμόσϕαιρα του πλανήτη παύει να περιέχει αυτό το συγκεκριμένο αέριο. Ενα άλλο σημαντικό συμπέρασμα της κινητικής θεωρίας είναι ότι τα ιδανικά αέρια υπακούουν στη λεγόμενη καταστατική εξίσωση των ιδανικών αερίων, p V = N k T, (1.14) όπου p είναι η πίεση, V ο όγκος, N το πλήθος των συστατικών σωματίων που απαρτίζουν το ιδανικό αέριο, T η απόλυτη θερμοκρασία, και k η σταθερά Boltzmann. 1.3 'Ennoiec apì th fusik tou fwtìc H fôsh tou fwtìc Το θεμελιώδες ερώτημα περί της ϕύσης του ϕωτός απασχόλησε πολύ τους ϕυσικούς. Στη διαλεύκανσή του συνετέλεσαν, μεταξύ πολλών άλλων, οι Νεύτωνας, Huygens, Young, και Maxwell. Ο πρώτος τάχθηκε υπέρ της «σωματιδιακής ϕύσης» του ϕωτός. Οι άλλοι υποστήριξαν την «κυματική ϕύση» του ϕωτός. Σήμερα γίνεται αποδεκτό ότι το ϕώς έχει «διττή ϕύση», σωματιδιακή και κυματική.
5 1.3 Εννοιες από τη ϕυσική του ϕωτός 4 Οταν διατυπώθηκε η υπόθεση της κυματικής ϕύσης του ϕωτός, προέκυψε το πρόσθετο ερώτημα περί της ουσίας, της οποίας τα κύματα παράγουν το ϕως. Η απάντηση δόθηκε κατά τη δεκαετία του 1860 από μία συνεπή θεωρία, η οποία περιγράϕει τον ηλεκτρισμό και τον μαγνητισμό με ενιαίο τρόπο. Συγκεκριμένα, ο ϕυσικομαθηματικός James Clerk Maxwell κατάϕερε να περιγράψει όλες τις βασικές ιδιότητες του ηλεκτρισμού και μαγνητισμού με τέσσερεις διαϕορικές εξισώσεις, αποδεικνύοντας ουσιαστικά ότι οι ηλεκτρικές και μαγνητικές δυνάμεις είναι δύο όψεις του ίδιου ϕαινόμενου, δηλαδή του ηλεκτρομαγνητισμού. Ο Maxwell έδειξε ότι τα ηλεκτρικά και μαγνητικά πεδία πρέπει να διαδίδονται στον χώρο υπό μορϕή κυμάτων με κοινή ταχύτητα c. Υπέθεσε λοιπόν ότι αυτά ακριβώς τα ηλεκτρομαγνητικά κύματα συνιστούν το ϕως, δηλαδή παρατηρούνται ως ϕως, υπόθεση που επαληθεύθηκε από το πείραμα. Για τον λόγο αυτόν, το ϕως αναϕέρεται και ως ηλεκτρομαγνητική ακτινοβολία. Συγκεκριμένα, το ϕως αποτελείται από ένα ηλεκτρικό πεδίο και από ένα μαγνητικό πεδίο που ταλαντώνονται συγχρονισμένα επί δύο καθέτων μεταξύ τους επιπέδων (Σχ. 1.2). Το συνιστάμενο ηλεκτρομαγνητικό κύμα χαρακτηρίζεται από τρία μεγέθη. 1. Το «μήκος κύματος», λ, δηλαδή την απόσταση δύο διαδοχικών μεγίστων ή ελαχίστων. 2. Τη «συχνότητα», ν, δηλαδή τον αριθμό των μεγίστων ή ελαχίστων που διέρχονται από δεδομένο σημείο στη μονάδα του χρόνου. 3. Την «ταχύτητα διάδοσης», c. Τα τρία αυτά μεγέθη συνδέονται μεταξύ τους με τη σχέση c = λ ν. (1.15) Η πλέον ακριβής μέχρι σήμερα μέτρηση της ταχύτητας του ϕωτός, c, έχει δώσει την τιμή c = m s 1. (1.16) Σχήμα 1.2: Το ηλεκτρομαγνητικό κύμα. Ο ανθρώπινος οϕθαλμός ανιχνεύει μήκη κύματος από 700 nm (ερυθρό χρώμα) μέχρι 400 nm (ιώδες χρώμα υπενθυμίζεται ότι 1 nm = 10 9 m = 10 Å). Στο «ϕάσμα της ηλεκτρομαγνητικής ακτινοβολίας» (Σχ. 1.3) περιλαμβάνονται μήκη κύματος από πολλά χιλιόμετρα (μακρά ραδιοκύματα) μέχρι κλάσματα του ενός Å(ακτίνες γ). Από το ϕάσμα αυτό, δύο μόνον περιοχές διέρχονται ανεμπόδιστα από τη γήινη ατμόσϕαιρα. Η πρώτη περιοχή, με μήκη κύματος της τάξης των m, αναϕέρεται ως «οπτικό παράθυρο». Η δεύτερη περιοχή, με μήκη κύματος της τάξης των m, ονομάζεται «ραδιοϕωνικό παράθυρο».
6 1.3 Εννοιες από τη ϕυσική του ϕωτός 5 Σχήμα 1.3: Το ϕάσμα της ηλεκτρομαγνητικής ακτινοβολίας Fwteinìthta kai lamprìthta Οταν ένα σώμα εκπέμπει ηλεκτρομαγνητική ακτινοβολία, η «ολική ισχύς της ακτινοβολίας» (= αθροιστική ισχύς για όλα τα μήκη κύματος της εκπεμπόμενης ακτινοβολίας) αναϕέρεται ως ϕωτεινότητα (luminosity), L, του εν λόγω σώματος. Η ϕωτεινότητα έχει μονάδες ισχύος, οπότε στο σύστημα SI μετριέται σε W. Ως λαμπρότητα (brightness), b, ενός σώματος που εκπέμπει ηλεκτρομαγνητική ακτινοβολία, σε απόσταση r από το σώμα, ορίζεται η ροή ενέργειας της ηλεκτρομαγνητικής ακτινοβολίας στην απόσταση αυτή, b = L 4 π r 2. (1.17)
7 1.4 Εννοιες από τη ϕυσική του μέλανος σώματος 6 Η λαμπρότητα έχει μονάδες ροής ενέργειας, οπότε στο σύστημα SI μετριέται σε J m 2 s 1 ή, ισοδύναμα, σε W m 'Ennoiec apì th fusik tou mèlanoc s matoc Oi nìmoi pou dièpoun to mèlan s ma Σε πολλές περιπτώσεις το αίτιο της εκπομπής ηλεκτρομαγνητικής ακτινοβολίας από ένα σώμα είναι η θερμοκρασία του σώματος τότε η εκπεμπόμενη ακτινοβολία αναϕέρεται ως «θερμική ακτινοβολία» του σώματος αυτού. Για τη θεωρητική μελέτη της θερμικής ακτινοβολίας, ορίζεται ένα ιδανικό σώμα, του οποίου η επιϕάνεια απορροϕά πλήρως την προσπίπτουσα στο σώμα αυτό ακτινοβολία. Ενα τέτοιο σώμα ονομάζεται μέλαν σώμα. Τη συμπεριϕορά του μέλανος σώματος καθορίζουν οι ακόλουθοι νόμοι. Νόμος μετατόπισης του Wien. Χωρίς περιορισμό της γενικότητας, θεωρούμε ένα σϕαιρικό μέλαν σώμα ϕωτεινότητας L και ακτίνας R. Η λαμπρότητα στην επιϕάνεια του σώματος, b S, ονομάζεται «επιϕανειακή λαμπρότητα», b S = b(r) = L 4 π R 2. (1.18) Ως «ϕασματική συνάρτηση επιϕανειακής λαμπρότητας», b S,λ, ορίζεται η συνάρτηση που δίνει για μία τιμή λ του μήκος κύματος τη συνεισϕορά του στοιχειώδους εύρους μηκών κύματος μεταξύ λ και λ + dλ στην επιϕανειακή λαμπρότητα b S (Σχ. 1.4). Το μέγεθος αυτό έχει μονάδες ροής ενέργειας ανά μονάδα μήκους κύματος, οπότε στο σύστημα SI μετριέται σε J m 3 s 1 ή, ισοδύναμα, σε W m 3. Αθροίζοντας για όλα τα μήκη κύματος, βρίσκουμε την επιϕανειακή λαμπρότητα, b S = 0 b S,λ dλ. (1.19) Από το Σχήμα 1.4 ϕαίνεται ότι για μία τιμή του μήκους κύματος, λ max, η ϕασματική συνάρτηση επιϕανειακής λαμπρότητας γίνεται μέγιστη, (b S,λ ) max. Η τιμή αυτή ονομάζεται «χαρακτηριστικό χρώμα» ή «κυρίαρχο χρώμα» του μέλανος σώματος. Άν το χαρακτηριστικό χρώμα βρίσκεται στο ορατό μέρος του ϕάσματος (Σχ. 1.3), τότε αντιστοιχεί σε ένα συγκεκριμένο ορατό χρώμα. Από το σύνολο λοιπόν των ϕωτονίων που δέχεται ο οϕθαλμός του παρατηρητή, τα περισσότερα έχουν χρώμα ίδιο με το χαρακτηριστικό χρώμα του μέλανος σώματος. Το 1893, ο Wilhelm Wien διαπίστωσε πειραματικά ότι το χαρακτηριστικό χρώμα είναι αντιστρόϕως ανάλογο της απόλυτης θερμοκρασίας του μέλανος σώματος, λ max = C W T. (1.20) Η σταθερή ποσότητα C W που εμπλέκεται στην Εξίσωση 1.20 ονομάζεται «σταθερά του Wien» και έχει την τιμή C W = m K. (1.21) Νόμος των Stefan Boltzmann. Η σχέση που συνδέει την επιϕανειακή λαμπρότητα, b S, του μέλανος σώματος με την απόλυτη θερμοκρασία του, T, βρέθηκε πειραματικά από τον Josef Stefan περί το 1880 και αποδείχθηκε στη συνέχεια
8 1.4 Εννοιες από τη ϕυσική του μέλανος σώματος 7 Σχήμα 1.4: Φασματική συνάρτηση επιϕανειακής λαμπρότητας μέλανος σώματος. Η ερυθρή καμπύλη αντιστοιχεί σε θερμοκρασία T = 4000 K, η πράσινη σε T = 5000 K, και η κυανή σε T = 6000 K. Στην κυανή καμπύλη, λ max είναι το μήκος κύματος για το οποίο η ϕασματική συνάρτηση επιϕανειακής λαμπρότητας λαμβάνει μέγιστη τιμή, (b S,λ ) max. Αυτό το μήκος κύματος είναι το χαρακτηριστικό χρώμα ή κυρίαρχο χρώμα του μέλανος σώματος για τη συγκεκριμένη θερμοκρασία. Η σκιασμένη λωρίδα έχει εμβαδόν b S,λ dλ και παριστάνει τη συνεισϕορά του στοιχειώδους εύρους μηκών κύματος μεταξύ λ και λ+dλ στην επιϕανειακή λαμπρότητα. Το ολικό εμβαδόν της περιοχής που βρίσκεται μεταξύ της κυανής καπύλης και του οριζόντιου άξονα, μέχρι άπειρου μήκους κύματος, παριστάνει την επιϕανειακή λαμπρότητα, b S, που υπολογίζεται από την Εξίσωση Η ποσότητα αυτή δίνεται από τον νόμο των Stefan Boltzmann (Εξ. 1.22). Ομοια ισχύουν και για τις άλλες δύο καμπύλες του σχήματος. θεωρητικά από τον Ludwig Boltzmann. Σύμϕωνα με τη σχέση αυτή, η επιϕανειακή λαμπρότητα του μέλανος σώματος είναι ανάλογη της τέταρτης δύναμης της απόλυτης θερμοκρασίας του, b S = σ T 4. (1.22) Η σταθερά σ του νόμου αυτού ονομάζεται «σταθερά του Stefan» και έχει την τιμή σ = W m 2 K 4. (1.23) To mèlan s ma kai h ditt fôsh tou fwtìc Οταν αυξάνεται η θερμοκρασία του μέλανος σώματος, η ϕασματική συνάρτηση επιϕανειακής λαμπρότητας, b S,λ, γίνεται μεγαλύτερη για όλες τις τιμές του μήκους
9 1.4 Εννοιες από τη ϕυσική του μέλανος σώματος 8 κύματος, λ. Συγχρόνως, η αντίστοιχη καμπύλη μετατοπίζεται ολόκληρη προς τα μικρότερα μήκη κύματος. Την ίδια συμπεριϕορά έχει και το χαρακτηριστικό χρώμα, λ max, του μέλανος σώματος. Συγκεκριμένα, καθώς η θερμοκρασία του μέλανος σώματος αυξάνεται, αυτό μετακινείται προς το υπέρυθρο, ορατό, υπεριώδες, κ.ο.κ. Ο Max Planck κατάϕερε να περιγράψει εμπειρικά τη συμπεριϕορά της ϕασματικής συνάρτησης επιϕανειακής λαμπρότητας με χρήση της εξίσωσης b S,λ = C 1 1 ( λ 5 C2 exp λ T ), (1.24) 1 προσδιορίζοντας τις τιμές C 1 = J m 2 s 1 και C 2 = m K για τις δύο σταθερές της Εξίσωσης Πολλοί ϕυσικοί, μεταξύ των οποίων και ο ίδιος ο Planck, προσπάθησαν να ερμηνεύσουν θεωρητικά τη χαρακτηριστική καμπύλη της ϕασματικής συνάρτησης επιϕανειακής λαμπρότητας (Σχ. 1.4, Εξ. 1.24). Προς τούτο, χρησιμοποίησαν ως αϕετηρία την ηλεκτρομαγνητική θεωρία του Maxwell υιοθέτησαν δηλαδή την κυματική ϕύση του ϕωτός. Ομως όλες οι σχετικές προσπάθειες απέβησαν άκαρπες. Αργότερα, περί το 1900, ο Planck επέτυχε να λύσει το πρόβλημα αυτό, στηριζόμενος σε δύο βασικές υποθέσεις. 1. Σωματιδιακή ϕύση του ϕωτός. Η ηλεκτρομαγνητική ενέργεια εκπέμπεται υπό μορϕή σωματιδίων ϕορέων, τα οποία ονομάζονται ϕωτόνια. 2. Εμπλοκή ιδιοτήτων από την κυματική ϕύση του ϕωτός. Η ενέργεια, E, ενός ϕωτονίου εξαρτάται από μεγέθη που σχετίζονται με την κυματική ϕύση του ϕωτός. Συγκεκριμένα, η ενέργεια αυτή είναι αντιστρόϕως ανάλογη του μήκους κύματος της ηλεκτρομαγνητικής ακτινοβολίας, η οποία έχει εκπεμψει το ϕωτόνιο, E = h c λ. (1.25) Η σταθερα h της σχέσης αυτής έχει την τιμή h = J s (1.26) και ονομάζεται σταθερά του Planck. Από την Εξίσωση 1.15 συνάγεται ότι η σχέση 1.25 μπορεί να λάβει τη μορϕή E = h ν. (1.27) Συνεπώς, η ενέργεια ενός ϕωτονίου είναι ανάλογη της συχνότητας, ν, ή, ισοδύναμα, αντιστρόϕως ανάλογη του μήκους κύματος, λ, της ηλεκτρομαγνητικής ακτινοβολίας, η οποία έχει εκπέμψει το ϕωτόνιο. Η σχέση αυτή αναϕέρεται ως νόμος του Planck και εδράζεται πλέον στη διττή ϕύση του ϕωτός, κυματική και σωματιδιακή. Πράγματι, το ϕως περιγράϕεται ως ροή σωματιδίων, των ϕωτονίων. Συγχρόνως, όμως, το κάθε ϕωτόνιο έχει ενέργεια που υπολογίζεται από τις κυματικές ιδιότητες του ϕωτός! Οι ενέργειες των ϕωτονίων είναι πολύ μικρές, οπότε εκϕράζονται με μονάδα μέτρησης το «ηλεκτρονιο βόλτ» (ev 1 ev = J). Με μονάδα ενέργειας το ev, η σταθερά του Planck έχει την τιμή h = ev s. (1.28)
10 1.5 Προκαταρκτικές γνώσεις για τα ϕάσματα 9 Ο Planck, έχοντας στη διάθεσή του το νέο θεωρητικό υπόβαθρο, κατάϕερε να αποδείξει την Εξίσωση 1.24, οπότε και επιβεβαίωσε θεωρητικά τη μορϕή που έχει η ϕασματική συνάρτηση επιϕανειακής λαμπρότητας μέλανος σώματος (Σχ. 1.4). Μέσω της απόδειξης αυτής, ταυτοποίησε τις δύο σταθερές της Εξίσωσης 1.24 με τις ποσότητες C 1 = 2 π h c 2 και C 2 = h c k. Στη βιβλιογραϕία, αρκετά συχνά αποκαλείται νόμος του Planck η Εξίσωση 1.24 και όχι η Εξίσωση Για να μη δημιουργείται σύγχυση, είναι προτιμότερο να αναϕέρεται η Εξίσωση 1.24 ως νόμος του Planck για τη ϕασματική συνάρτηση και η Εξίσωση 1.27 ως νόμος του Planck για την ενέργεια των ϕωτονίων. 1.5 Prokatarktikèc gn seic gia ta fˆsmata Fˆsmata ekpomp c Είναι γνωστό από την οπτική ότι ο δείκτης διάθλασης μίας ηλεκτρομαγνητικής ακτινοβολίας εξαρτάται από το μήκος κύματος ή, ισοδύναμα, από τη συχνότητα της ακτινοβολίας αυτής. Άν η ηλεκτρομαγνητική ακτινοβολία αποτελείται από διαϕορετικές συχνότητες, όπως μία δέσμη λευκού ϕωτός, τότε αυτή χαρακτηρίζεται από αντίστοιχους διαϕορετικούς δείκτες διάθλασης. Το ϕαινόμενο αυτό ονομάζεται «διασκεδασμός». Εξαιτίας του διασκεδασμού, όταν δέσμη λευκού ϕωτός περάσει μέσα από ένα πρίσμα, αναλύεται σε έγχρωμη ταινία, η οποία αναϕέρεται ως «ϕάσμα» του λευκού ϕωτός. Τα όργανα, με τα οποία εξετάζονται τα ϕάσματα, ονομάζονται «ϕασματοσκόπια». Βασικό εξάρτημα του ϕασματοσκόπιου είναι το πρίσμα μέσα από το οποίο περνάει η εξεταζόμενη ϕωτεινή δέσμη. Μία ϕωτεινή πηγή εκπέμπει ηλεκτρομαγνητική ακτινοβολία, το ϕάσμα της οποίας ονομάζεται «ϕάσμα εκπομπής» της πηγής. Διακρίνουμε τα ακόλουθα ϕάσματα εκπομπής. 1. «Συνεχή ϕάσματα εκπομπής». Τα ϕάσματα αυτά εμϕανίζονται στο ϕασματοσκόπιο όταν εξετάζουμε το ϕως που εκπέμπουν διάπυρα (= υψηλής θερμοκρασίας) στερεά ή υγρά σώματα. Π.χ, το ϕως του ηλεκτρικού λαμπτήρα πυράκτωσης δίνει συνεχές ϕάσμα εκπομπής. Τα συνεχή ϕάσματα εκπομπής δεν μπορούν να μας δώσουν πληροϕορίες για τη χημική σύσταση των ϕωτεινών πηγών που τα εκπέμπουν, επειδή οι συγκεκριμένες ϕωτεινές πηγές προσομοιάζουν με μέλανα σώματα ( 1.4) και έτσι έχουν κοινά χαρακτηριστικά. 2. «Γραμμικά ϕάσματα εκπομπής». Στις λεγόμενες ψυχρές ϕωτεινές πηγές, το ϕως παράγεται με τη διέγερση (μέσω διέλευσης ηλεκτρικού ρεύματος) των ατόμων αερίων ή ατμών κατάλληλων χημικών στοιχείων. Στο ϕασματοσκόπιο, το ϕως αυτό αναλύεται σε διακριτές έγχρωμες γραμμές που λέγονται «ϕασματικές γραμμές εκπομπής» και συνθέτουν ένα γραμμικό ϕάσμα εκπομπής. Επίσης, διάπυρα αέρια ή ατμοί χημικών στοιχείων δίνουν γραμμικά ϕάσματα εκπομπής. Ενώ διάπυρα αέρια ή ατμοί που αποτελούνται από μόρια δίνουν «ταινιωτά ϕάσματα εκπομπής», δηλαδή διευρυμένες ϕασματικές γραμμές υπό μορϕήν ταινιών που λέγονται «ϕασματικές ταινίες εκπομπής». Τα γραμμικά ϕάσματα εκπομπής είναι χαρακτηριστικά των αερίων ή ατμών που τα εκπέμπουν. Επομένως μπορούν να μας δώσουν πληροϕορίες για τη χημική σύσταση των αντίστοιχων ϕωτεινών πηγών. Για να μελετήσουμε το γραμμικό ϕάσμα εκπομπής ενός χημικού στοιχείου,
11 1.5 Προκαταρκτικές γνώσεις για τα ϕάσματα 10 που σε συνήθεις συνθήκες είναι στερεό, το θερμαίνουμε σε υψηλή θερμοκρασία και έτσι το μετατρέπουμε σε ατμούς. Π.χ., οι ατμοί του νατρίου εκπέμπουν δύο έντονες κίτρινες ϕασματικές γραμμές, οι οποίες βρίσκονται πολύ κοντά μεταξύ τους (λ NaI = nm και λ NaII = nm). Επίσης οι ατμοί του χαλκού, που μπορούμε να πάρουμε από βολταϊκό τόξο με χάλκινα ηλεκτρόδια, δίνουν στο ϕασματοσκόπιο πολλές ϕασματικές γραμμές, από τις οποίες η πιο έντονη έχει πράσινο χρώμα Fˆsmata aporrìfhshc Εστω ότι τοποθετούμε μεταξύ μίας πηγής λευκού ϕωτός και του ϕασματοσκόπιου ένα έγχρωμο υγρό ή μία εγχρωμη γυάλινη πλάκα. Το αποτέλεσμα είναι να εμϕανίζεται έντονα το χαρακτηριστικό χρώμα του «απορροϕητικού υλικού» (δηλαδή του υγρού ή της πλάκας) στο υπόβαθρο του συνεχούς ϕάσματος εκπομπής, αλλά τα υπόλοιπα τμήματα του υπόβαθρου να έχουν αντικατασταθεί από σκοτεινές περιοχές. Τέτοια ϕάσματα ονομάζονται «ϕάσματα απορρόϕησης». Διακρίνουμε τα ακόλουθα ϕάσματα απορρόϕησης. 1. «Συνεχή ϕάσματα απορρόϕησης». Εδώ το απορροϕητικό υλικό είναι ένα έγχρωμο στερεό ή υγρό, το οποίο απορροϕά ορισμένες ευρείες συνεχείς περιοχές του συνεχούς ϕάσματος. 2. «Γραμμικά ϕάσματα απορρόϕησης». Οταν μεταξύ μίας πηγής λευκού ϕωτός και του ϕασματοσκόπιου παρεμβάλλονται αέρια ή ατμοί χημικού στοιχείου χαμηλής θερμοκρασίας, τότε στο υπόβαθρο του συνεχούς ϕάσματος εμϕανίζονται ορισμένες σκοτεινές «γραμμές απορρόϕησης» στις θέσεις ακριβώς που θα εμϕανίζονταν οι αντίστοιχες ϕασματικές γραμμές εκπομπής των συγκεκριμένων αερίων ή ατμών σε διάπυρη κατάσταση. Π.χ, άν παρεμβληθούν ατμοί νατρίου, τότε εμϕανίζονται οι δύο γραμμές απορρόϕησης, λ NaI και λ NaII, του κίτρινου χρώματος. Οταν η χημική ουσία που παρεμβάλλεται αποτελείται από μόρια, τότε στο υπόβαθρο του συνεχούς ϕάσματος εμϕανίζονται ορισμένες σκοτεινές «ταινίες απορρόϕησης» στις θέσεις ακριβώς που θα εμϕανίζονταν οι αντίστοιχες ϕασματικές ταινίες εκπομπής της συγκεκριμένης χημικής ουσίας σε διάπυρη κατάσταση.
12 Kefˆlaio 2 'Ennoiec apì th fusik twn astèrwn 2.1 Fainìmenec lamprìthtec kai fainìmena megèjh Από ενεργειακή άποψη, οι αστέρες θεωρούνται εξωτικές μηχανές παραγωγής ενέργειας. Η ολική ισχύς ενός αστέρα είναι το άθροισμα: (1) της ϕωτεινότητας του αστέρα ( 1.3.2), (2) της ισχύος που οϕείλεται στην έκλυση νετρίνων από τον αστέρα, και (3) της ισχύος που οϕείλεται στην απώλεια μάζας του αστέρα. Στην αστροϕυσική, μεγάλη σημασία έχει η πρώτη συνιστώσα της ολικής ισχύος, δηλαδή η ϕωτεινότητα. Η λαμπρότητα, b, ενός αστέρα (Εξ. 1.17) εξαρτάται τόσο από την ϕωτεινότητά του, L, όσο και από την απόσταση παρατήρησης, r. Στην επιϕάνεια του αστέρα (ακτίνας R) η λαμπρότητα είναι ίση με την επιϕανειακή λαμπρότητά του (Εξ. 1.18). Για να δοθεί έμϕαση στο γεγονός ότι η λαμπρότητα είναι σχετικό και όχι απόλυτο μέγεθος, χρησιμοποιείται ο όρος ϕαινόμενη λαμπρότητα (apparent brightness), που υποδηλώνει ότι η ποσότητα αυτή μετριέται όπως ϕαίνεται από έναν παρατηρητή σε απόσταση r από τον αστέρα. Ο ανθρώπινος οϕθαλμός λειτουργεί ως όργανο μέτρησης της ϕαινόμενης λαμπρότητας. Δεν έχει όμως μεγάλη ικανότητα στο να διακρίνει ως διαϕορετικές δύο παραπλήσιες τιμές ϕαινόμενης λαμπρότητας. Τούτο οϕείλεται στο γεγονός ότι ο οϕθαλμός δεν αποκρίνεται γραμμικά στα οπτικά ερεθίσματα, αλλά λογαριθμικά. Η συγκεκριμένη οπτική συμπεριϕορά αποτελεί μερική περίπτωση του ψυχοϕυσικού νόμου των Weber Fechner, ο οποίος διατυπώνεται ως εξής. WF. Η ένταση οποιουδήποτε υποκειμενικού αισθήματος εξαρτάται λογαριθμικά από την ένταση του αντίστοιχου ερεθίσματος. Στην περίπτωση παρατήρησης ενός αστέρα, το ερέθισμα (δηλαδή το αίτιο) είναι η ϕαινόμενη λαμπρότητα του αστέρα. Ενώ το υποκειμενικό αίσθημα (δηλαδή το αποτέλεσμα) που δημιουργείται στον οϕθαλμό ονομάζεται ϕαινόμενο μέγεθος (apparent magnitude) του αστέρα. Περί το 140 π.χ., ο Ιππαρχος κατέταξε τους αστέρες σε έξι ϕαινόμενα μεγέθη. Συγκεκριμένα, ονόμασε «αστέρες πρώτου μεγέθους» τους πιο λαμπρούς, «αστέ- 11
13 2.1 Φαινόμενες λαμπρότητες και ϕαινόμενα μεγέθη 12 ρες δευτέρου μεγέθους» τους αμέσως αμυδρότερους, κ.ο.κ., μέχρι και τους «αστέρες έκτου μεγέθους» αμυδρότεροι αστέρες δεν είναι δυνατό να παρατηρηθούν δια γυμνού οϕθαλμού. Η ταξινόμηση αυτή ονομάζεται κλίμακα μεγεθών του Ιππάρχου. Στην εποχή μας, η κλίμακα των ϕαινομένων μεγεθών έχει επεκταθεί εκατέρωθεν της αρχικής, ώστε να συμπεριληϕθούν λαμπρότερα σώματα, όπως ο Ηλιος, καθώς και πολύ αμυδροί αστέρες παρατηρούμενοι με τηλεσκόπια. Η μέτρηση των ϕαινομένων μεγεθών γίνεται πλέον με όργανα υψηλής ακρίβειας. Ως παραδείγματα από τη διευρυμένη κλίμακα αναϕέρονται ο Ηλιος που έχει ϕαινόμενο μέγεθος 26.8, η Σελήνη 12.7, η Αϕροδίτη 4.4, ο Δίας 2.7, ο Άρης 2.0, ο αστέρας α του Μεγάλου Κυνός (α CMa: Sirius) 1.46, ο Κρόνος 0.3, ο αστέρας α του Κενταύρου (α Cen: Rigil Kentaurus) 0.01, ο αστέρας α του Ωρίωνα (α Ori: Betelgeuse) +0.50, ο αστέρας α του Σκορπιού (α Sco: Antares) +0.96, ο αστέρας β του Νοτίου Σταυρού (β Cru: Mimosa) +1.25, ο αστέρας ϵ του Ηριδανού (ϵ Eri) +3.73, ο αστέρας ϵ του Ινδού (ϵ Ind) +4.69, και ο Πλούτωνας Άν b m και b n είναι οι ϕαινόμενες λαμπρότητες που αντιστοιχούν στα ϕαινόμενα μεγέθη m και n, τότε, σύμϕωνα με τον ψυχοϕυσικό νόμο των Weber Fechner, b m b n = C n m WF. (2.1) Για τον προσδιορισμό της σταθεράς C WF, κάνουμε χρήση του γεγονότος ότι στο πρώτο ϕαινόμενο μέγεθος της κλίμακας μεγεθών αντιστοιχεί ϕαινόμενη λαμπρότητα, b 1, εκατό ϕορές μεγαλύτερη από τη λαμπρότητα που αντιστοιχεί στο έκτο ϕαινόμενο μέγεθος, b 6 το γεγονός αυτό είναι γνωστό από την παρατήρηση. Οπότε ισχύει ή b 1 b 6 = 100 = C 6 1 WF = C 5 WF, (2.2) C WF = = (2.3) Αντικαθιστώντας στην Εξίσωση 2.1 την τιμή της σταθεράς C WF (Εξ. 2.3), λογαριθμίζοντας, και εκτελώντας τις ενδιάμεσες πράξεις, βρίσκουμε ( ) bm n m = 2.5 log. (2.4) Εϕαρμόζουμε την Εξίσωση 2.4 για δύο αστέρες με ϕαινόμενα μεγέθη n = +9 και m = 1. Συγκεκριμένα, έχουμε ( ) b 1 log = 9 ( 1) = 4, (2.5) 2.5 ή b +9 b n b 1 = 10 4 b +9. (2.6) Ωστε ένας αστέρας με ϕαινόμενο μέγεθος 1 έχει ϕορές μεγαλύτερη ϕαινόμενη λαμπρότητα από έναν αστέρα με ϕαινόμενο μέγεθος +9.
14 2.2 Απόλυτες λαμπρότητες και απόλυτα μεγέθη Apìlutec lamprìthtec kai apìluta megèjh OrismoÐ Για να εξετάσουμε κατά πόσον ένας αστέρας είναι κατ απόλυτο τρόπο (και όχι κατά σχετικό τρόπο) λαμπρότερος από έναν άλλο, πρέπει να τους θεωρήσουμε στην ίδια «πρότυπη απόσταση», r 10. Η απόσταση αυτή έχει ορισθεί, με διεθνή συμϕωνία, ίση προς (βλέπε και Εξ. 1.7) r 10 = 10 pc = km = m. (2.7) Οι προκύπτουσες τιμές για τη λαμπρότητα και το μέγεθος ονομάζονται απόλυτη λαμπρότητα (absolute brightness), B, και απόλυτο μέγεθος (absolute magnitude), M, αντίστοιχα. Η σχέση μεταξύ του ϕαινόμενου μεγέθους, m, και του απόλυτου μεγέθους, M, ενός αστέρα βρίσκεται ως εξής. Ο λόγος των αντίστοιχων λαμπροτήτων του παρατηρούμενου αστέρα είναι (βλέπε και Εξ. 1.17) ( ) L b B = 4πr ( 2 L 4πr 2 10 ) = 102 r 2 = 100 r 2. (2.8) Πρέπει να προσεχθεί ιδιαίτερα το γεγονός ότι, αϕού το r 10 αντικαταστάθηκε σε παρσέκ, η απόσταση r αντικαθίσταται ή υπολογίζεται και αυτή σε παρσέκ. Στην Εξίσωση 2.4 θέτουμε n = M, m = m, b n = B, και b m = b εϕαρμόζουμε δηλαδή την εξίσωση αυτή για δύο αστέρες, από τους οποίους ο πρώτος παριστάνει ακριβώς τον παρατηρούμενο αστέρα, ενώ ο δεύτερος παριστάνει τον ίδιο αστέρα, παρατηρούμενο όμως από την πρότυπη απόσταση των 10 pc. Χρησιμοποιώντας και το αποτέλεσμα της Εξίσωσης 2.8, βρίσκουμε ( ) 100 M m = 2.5 log, (2.9) η οποία, μετά την εκτέλεση των πράξεων, λαμβάνει τη μορϕή r 2 M = m log(r). (2.10) Στην εξίσωση αυτή, όπως αναϕέρθηκε και προηγουμένως, η απόσταση r αντικαθίσταται ή υπολογίζεται σε παρσέκ Apìluto mègejoc kai apìluth lamprìthta tou 'Hliou Στην περίπτωση του Ηλιου, θέτουμε στην Εξίσωση 2.10 m = 26.8 και r = a E = 1 AU = pc (βλέπε και Εξς ) οπότε βρίσκουμε ( ) 1 M = log = (2.11) Άν λοιπόν παρατηρούσαμε τον Ηλιο από απόσταση 10 pc, θα τον βλέπαμε σαν έναν αστέρα πέμπτου μεγέθους.
15 2.2 Απόλυτες λαμπρότητες και απόλυτα μεγέθη 14 Η ϕωτεινότητα του Ηλιου, L, είναι L = W, (2.12) οπότε η απόλυτη λαμπρότητά του, B, προκύπτει ίση με B = L 4πr 2 10 = J m 2 s 1. (2.13) Για έναν γήινο παρατηρητή ο Ηλιος έχει ϕαινόμενη λαμπρότητα, b,e, ίση με L b,e = 4πa 2 E = J m 2 s 1 = 1370 W m 2. (2.14) Δεδομένου ότι η ακτίνα του Ηλιου, R, είναι R = km = m, (2.15) η επιϕανειακή του λαμπρότητα, b S, υπολογίζεται ίση με L b S = 4πR 2 = J m 2 s 1. (2.16) Apìluth lamprìthta kai fwteinìthta enìc astèra upologizìmenec sunart sei twn antðstoiqwn hliak n posot twn Για να υπολογίσουμε την απόλυτη λαμπρότητα, B, ενός αστέρα (με απόλυτο μέγεθος M) χρησιμοποιώντας ως μονάδα μέτρησης την ηλιακή απόλυτη λαμπρότητα (Εξ. 2.13), B, εργαζόμαστε ως εξής. Εϕαρμόζουμε την Εξίσωση 2.4 για τον συγκεκριμένο αστέρα και τον Ηλιο θεωρώντας ότι και οι δύο βρίσκονται στην πρότυπη απόσταση των 10 pc. Στην απόσταση αυτή, οι ϕαινόμενες λαμπρότητες και τα ϕαινόμενα μεγέθη συμπίπτουν με τις απόλυτες λαμπρότητες και τα απόλυτα μεγέθη θέτουμε λοιπόν n = M = (Εξ. 2.11), m = M, b n = B, και b m = B. Ο λόγος B = B/B παριστάνει την απόλυτη λαμπρότητα του αστέρα μετρούμενη με μονάδα μέτρησης την ηλιακή απόλυτη λαμπρότητα. Μετά τις αντικαταστάσεις και την εκτέλεση των πράξεων, η Εξίσωση 2.4 γίνεται ή log(b) = M, (2.17) B = 10 ( M). (2.18) Για να εκϕράσουμε το αποτέλεσμα αυτό στο σύστημα SI, πρέπει να το πολλαπλασιάσουμε επί B (Εξ. 2.13), B = B B. (2.19) Επίσης, επειδή ( L ) B B = 4 π r10 2 ) = L, (2.20) L ( L 4 π r 2 10
16 2.3 Θερμοκρασία και χρώμα 15 η Εξίσωση 2.17 δίνει συγχρόνως και τη ϕωτεινότητα, L = L/L, του συγκεκριμένου αστέρα μετρούμενη με μονάδα μέτρησης την ηλιακή ϕωτεινότητα (Εξ 2.12). Εϕαρμόζουμε τη σχέση αυτή για τον αστέρα ϵ Eri που βρίσκεται σε απόσταση r = 3.28 pc και έχει ϕαινόμενο μέγεθος m = οπότε το απόλυτο μέγεθός του είναι M = log(3.28) = (Εξ. 2.10). Με αντικατάσταση των δεδομένων, η Εξίσωση 2.17 γίνεται log(l) = = (2.21) Οπότε L = Δηλαδή ο αστέρας ϵ Eri έχει ϕωτεινότητα 3.3 ϕορές μικρότερη από την ηλιακή ϕωτεινότητα. Για να εκϕράσουμε το αποτέλεσμα αυτό στο σύστημα SI, πρέπει να το πολλαπλασιάσουμε επί L (Εξ. 2.12), L = L L = W = W. (2.22) 2.3 JermokrasÐa kai qr ma JermokrasÐa qr matoc kai energìc jermokrasða Επειδή οι αστέρες συμπεριϕέρονται ως μέλανα σώματα, οι νόμοι που διέπουν το μέλαν σώμα ( 1.4.1) μπορούν να χρησιμοποιηθούν στην εκτίμηση της επιϕανειακής θερμοκρασίας ενός αστέρα. Η εκτίμηση που προκύπτει από τον νόμο μετατόπισης του Wien ονομάζεται «θερμοκρασία χρώματος» (colour temperature), T c, ενώ η εκτίμηση που προκύπτει από τον νόμο των Stefan Boltzmann ονομάζεται «ενεργός θερμοκρασία» (effective temperature), T e, ενός αστέρα. Συγκεκριμένα, θερμοκρασία χρώματος ενός αστέρα είναι η θερμοκρασία που πρέπει να έχει το μέλαν σώμα, ώστε το χαρακτηριστικό χρώμα του, λ max, να συμπίπτει με το παρατηρούμενο χαρακτηριστικό χρώμα του αστέρα. Επίσης, ενεργός θερμοκρασία ενός αστέρα είναι η θερμοκρασία που πρέπει να έχει το μέλαν σώμα, ώστε η επιϕανειακή λαμπρότητά του, b S, να συμπίπτει με την παρατηρούμενη επιϕανειακή λαμπρότητα του αστέρα. Για να υπολογισθεί η θερμοκρασία χρώματος, T c, πρέπει να είναι γνωστή η τιμή λ max του μήκους κύματος, για την οποία η ϕασματική συνάρτηση επιϕανειακής λαμπρότητας γίνεται μέγιστη, (b S,λ ) max δηλαδή πρέπει να είναι γνωστό το χαρακτηριστικό χρώμα του αστέρα. Στην περίπτωση του Ηλιου, έχουμε λ max = 500 nm = m. (2.23) Λύνοντας τον νόμο μετατόπισης του Wien (Εξ. 1.20) ως προς τη θερμοκρασία και αντικαθιστώντας τα δεδομένα, βρίσκουμε T c = C W = λ max K = 5800 K. (2.24) Για τον υπολογισμό της ενεργού θερμοκρασίας, T e, πρέπει να είναι γνωστή η ϕαινόμενη λαμπρότητα, b, και το γωνιακό μέγεθος, α, του παρατηρούμενου αστέρα. Συγκεκριμένα, από τη σχέση ορισμού της λαμπρότητας (Εξ. 1.17), έχουμε b = L 4 π r 2 = 4 πr2 σ T 4 e 4 π r 2 = 1 4 ( ) 2 2R σ Te 4 = 1 r 4 α2 σ Te 4. (2.25)
17 2.3 Θερμοκρασία και χρώμα 16 Στην εξίσωση αυτή έχουμε αντικαταστήσει τη ϕωτεινότητα, L, με το γινόμενο του επιϕανειακού εμβαδού, 4πR 2 (όπου R η ακτίνα του αστέρα), επί την επιϕανειακή λαμπρότητα, b S επίσης έχουμε χρησιμοποιήσει τον νόμο των Stefan Boltzmann (Εξ. 1.22), για να εκϕράσουμε την b S ως συνάρτηση της T e. Στη συνέχεια έχουμε εισαγάγει το γωνιακό μέγεθος, α, του αστέρα (Εξ. 1.2, με D = 2R και d = r). Λύνοντας την Εξίσωση 2.25 ως προς T e, βρίσκουμε T e = 4 4 b α 2 σ. (2.26) Στην περίπτωση του Ηλιου, έχουμε b,e = W m 2 (Εξ. 2.14) και α,e = 2R a E (Εξς. 1.6, 2.15). Αντικαθιστώντας τα δεδομένα στην Εξίσωση 2.26, βρίσκουμε T e 5790 K. (2.27) Fainìmeno qr ma Το «ϕαινόμενο χρώμα» ενός αστέρα είναι το αίσθημα που δημιουργείται στον οϕθαλμό του παρατηρητή από όλα τα μήκη κύματος του ορατού ϕάσματος του αστέρα. Μπορεί βέβαια το οπτικό αυτό αίσθημα να επηρεάζεται καθοριστικά από το χαρακτηριστικό χρώμα του αστέρα ( 1.4.1), αλλά τελικά ο οϕθαλμός δεν ταυτίζει το ϕαινόμενο χρώμα με το χαρακτηριστικό χρώμα. Πρέπει να τονισθεί μάλιστα ότι το ϕαινόμενο χρώμα είναι το αίσθημα που δημιουργείται από πολλά μήκη κύματος, ενώ το χαρακτηριστικό χρώμα είναι ένα και μόνον ένα μήκος κύματος ή, όπως αλλοιώς λέμε, μία «μονοχρωματική ακτινοβολία». Εξάλλου το χαρακτηριστικό χρώμα μπορεί να μη βρίσκεται καν στην ορατή περιοχή του ϕάσματος, δηλαδή να μην αποτελεί καν ορατό χρώμα. Το ϕαινόμενο χρώμα ενός αστέρα εξαρτάται από την επιϕανειακή θερμοκρασία του για τους εξής λόγους. Ενας σχετικά ψυχρός αστέρας (T 3000 K, Σχ. 2.1) έχει το χαρακτηριστικό χρώμα του στην υπέρυθρή περιοχή του ϕάσματος. Αυτό που αντιλαμβάνεται ο οϕθαλμός ως ϕαινόμενο χρώμα είναι το ερέθισμα από τα μήκη κύματος του ορατού ϕάσματος που βρίσκονται προς την πλευρά του χαρακτηριστικού χρώματος, επειδή σε εκείνη την πλευρά οι τιμές της ϕασματικής συνάρτησης επιϕανειακής λαμπρότητας είναι μεγαλύτερες. Τούτο σημαίνει ότι ο οϕθαλμός δέχεται πολλά ερυθρά ϕωτόνια, λιγότερα πορτοκαλί ϕωτόνια, ακόμη λιγότερα κίτρινα ϕωτόνια, κ.ο.κ. Οπότε ο παρατηρητής βλέπει τον αστέρα να έχει χρώμα ερυθρό. Στη συνέχεια, ένας αστέρας μέσης θερμοκρασίας (T 5800 K, Σχ. 2.2), όπως ο Ηλιος, έχει το χαρακτηριστικό χρώμα του στο μέσο περίπου του ορατού ϕάσματος. Αυτό σημαίνει ότι, εκατέρωθεν του λ max, οι τιμές της ϕασματικής συνάρτησης επιϕανειακής λαμπρότητας είναι συγκρίσιμες. Ετσι ο οϕθαλμός δέχεται περίπου ίσο αριθμό κυανών ϕωτονίων, πράσινων ϕωτονίων, κίτρινων ϕωτονίων, κ.ο.κ. Το αποτέλεσμα είναι να βλέπει ο παρατηρητής έναν κιτρινόλευκο αστέρα. Τέλος, ένας σχετικά θερμός αστέρας (T K, Σχ. 2.3) έχει το χαρακτηριστικό χρώμα του στην υπεριώδη περιοχή του ϕάσματος. Αυτό που αντιλαμβάνεται ο οϕθαλμός ως ϕαινόμενο χρώμα είναι το ερέθισμα από τα μήκη κύματος του ο- ρατού ϕάσματος που βρίσκονται προς την πλευρά του χαρακτηριστικού χρώματος, επειδή σε εκείνη την πλευρά οι τιμές της ϕασματικής συνάρτησης επιϕανειακής λαμπρότητας είναι μεγαλύτερες. Συνεπώς ο οϕθαλμός δέχεται πολλά κυανά ϕωτόνια, λιγότερα πράσινα ϕωτόνια, ακόμη λιγότερα κίτρινα ϕωτόνια, κ.ο.κ. Οπότε ο παρατηρητής βλέπει τον αστέρα να έχει χρώμα κυανό.
18 2.4 Το ηλιακό ϕάσμα 17 Σχήμα 2.1: Φασματική συνάρτηση επιϕανειακής λαμπρότητας για αστέρα επι- ϕανειακής θερμοκρασίας Τ=3000 Κ. Το χαρακτηριστικό χρώμα του αστέρα, λ max 965 nm, βρίσκεται στο υπέρυθρο του ϕάσματος έτσι ολόκληρο το ορατό ϕάσμα βρίσκεται αριστερά του λ max. Τα πλησιέστερα προς το χαρακτηριστικό χρώμα μήκη κύματος του ορατού ϕάσματος δίνουν μεγαλύτερες τιμές για τη ϕασματική συνάρτηση. Αυτό σημαίνει ότι στον οϕθαλμό του παρατηρητή προσπίπτουν πολλά ερυθρά ϕωτόνια, λιγότερα πορτοκαλί ϕωτόνια, ακόμη λιγότερα κίτρινα ϕωτόνια, κ.ο.κ. Οπότε το ϕαινόμενο χρώμα του αστέρα είναι το ερυθρό. Επιλέγοντας τα χρώματα ερυθρό και κυανό, τα οποία βρίσκονται στα δύο άκρα του ορατού ϕάσματος, μπορούμε να διατυπώσουμε τον ακόλουθο γενικό κανόνα που συσχετίζει την επιϕανειακή θερμοκρασία των αστέρων με το ϕαινόμενο χρώμα τους. Κανόνας TC. Οι ερυθροί αστέρες είναι σχετικά ψυχροί με χαμηλές επιϕανειακές θερμοκρασίες, ενώ οι κυανοί αστέρες είναι σχετικά θερμοί με υψηλές επιϕανειακές θερμοκρασίες. 2.4 To hliakì fˆsma Η «ϕωτόσϕαιρα» αποτελείται από τα εξωτερικά αέρια στρώματα του Ηλιου, από τα οποία εκπέμπεται ηλεκτρομαγνητική ακτινοβολία. Είναι δηλαδή μία επιδερμική ζώνη ακτινοβολίας πάχους 400 km. Η ϕωτόσϕαιρα περιβάλλεται από ένα αραιό αέριο στρώμα, το οποίο ονομάζεται «χρωμόσϕαιρα». Αυτή εκτείνεται σε ύψος km υπεράνω της ϕωτόσϕαιρας. Η μέση πυκνότητά της είναι 2500 ϕορές μικρότερη από τη μέση πυκνότητα της ϕωτόσϕαιρας. Με τη βοήθεια του ϕασματοσκόπιου διαπιστώνουμε ότι ο Ηλιος εκπέμπει ένα γραμμικό ϕάσμα απορρόϕησης. Τούτο οϕείλεται στους εξής παράγοντες. Η ϕωτόσϕαιρα έχει πολύ υψηλή θερμοκρασία και εκπέμπει ηλεκτρομαγνητική ακτινοβολία
19 2.5 Φασματική ταξινόμηση των αστέρων 18 Σχήμα 2.2: Φασματική συνάρτηση επιϕανειακής λαμπρότητας για αστέρα επι- ϕανειακής θερμοκρασίας Τ=5800 Κ. Το χαρακτηριστικό χρώμα του αστέρα, λ max 500 K, βρίσκεται περίπου στο μέσο του ορατού ϕάσματος. Οπότε ο οϕθαλμός δέχεται περίπου ίσο αριθμό ϕωτονίων διαϕόρων χρωμάτων και αντιλαμβάνεται τον αστέρα ως κιτρινόλευκο. όπως ένα μέλαν σώμα θερμοκρασίας 6000 K (βλέπε και Εξς. 2.24, 2.27 επίσης Σχ. 1.4). Η ηλεκτρομαγνητική ακτινοβολία συνεχούς ϕάσματος της ϕωτόσϕαιρας περνάει στη συνέχεια μέσα από τη χρωμόσϕαιρα. Αυτή αποτελείται από αέρια και ατμούς χαμηλής θερμοκρασίας σε σύγκριση με τη θερμοκρασία της ϕωτόσϕαιρας. Ετσι ορισμένα χαρακτηριστικά μήκη κύματος των αερίων και ατμών προκαλούν αντίστοιχες γραμμές απορρόϕησης επί του συνεχούς ϕάσματος της ϕωτόσϕαιρας, με αποτέλεσμα το ηλιακό ϕάσμα να εμϕανίζεται ως γραμμικό ϕάσμα απορρόϕησης. Περί το 1815, ο Joseph von Fraunhofer παρατήρησε με το ϕασματοσκόπιό του τις πιο έντονες γραμμές απορρόϕησης του ηλιακού ϕάσματος, τις οποίες και ονόμασε με τα γράμματα A, B, C, D, E, κ.ο.κ. Η γραμμή D αντιστοιχεί στη ϕασματική γραμμή λ NaI του νατρίου. Ομως μερικές γραμμές, όπως οι A και B, δεν είναι μονοχρωματικές αλλά διευρυμένες αποτελούν δηλαδή ταινίες απορρόϕησης, οι οποίες αντιστοιχούν σε ταινίες εκπομπής διαϕόρων μορίων (όπως το νερό και το διοξείδιο του άνθρακα) της γήινης ατμόσϕαιρας, από την οποία διέρχεται το ηλιακό ϕως. 2.5 Fasmatik taxinìmhsh twn astèrwn Τα ϕάσματα των αστέρων είναι παρόμοια με το ηλιακό ϕάσμα. Εμϕανίζουν δηλαδή διάϕορες σκοτεινές γραμμές απορρόϕησης επάνω στο συνεχές ϕάσμα που εκπέμ-
20 2.5 Φασματική ταξινόμηση των αστέρων 19 Σχήμα 2.3: Φασματική συνάρτηση επιϕανειακής λαμπρότητας για αστέρα επι- ϕανειακής θερμοκρασίας Τ=10000 Κ. Το χαρακτηριστικό χρώμα του αστέρα, λ max 290 nm, βρίσκεται στο υπεριώδες του ϕάσματος. Ολόκληρο το ορατό ϕάσμα βρίσκεται δεξιά του λ max. Τα εγγύτερα προς το χαρακτηριστικό χρώμα μήκη κύματος του ορατού ϕάσματος δίνουν μεγαλύτερες τιμές για τη ϕασματική συνάρτηση. Ετσι ο οϕθαλμός δέχεται πολλά κυανά ϕωτόνια, λιγότερα πράσινα ϕωτόνια, ακόμη λιγότερα κίτρινα ϕωτόνια, κ.ο.κ. Οπότε το ϕαινόμενο χρώμα του αστέρα είναι το κυανό. πεται από τις αστρικές ϕωτόσϕαιρες. Ορισμένα αστρικά ϕάσματα εμϕανίζουν και σκοτεινές ταινίες απορρόϕησης, οι οποίες δείχνουν ότι στις συγκεκριμένες αστρικές χρωμόσϕαιρες υπάρχουν και μόρια. Οι γραμμές και οι ταινίες απορρόϕησης χαρακτηρίζουν τη χημική σύσταση ενός αστέρα. Ενώ το συνεχές ϕάσμα εκπομπής της ϕωτόσϕαιράς του εξαρτάται από την επιϕανειακή θερμοκρασία του. Η ταξινόμηση των αστέρων σε συγκεκριμένους «ϕασματικούς τύπους» γίνεται με κριτήριο την επιϕανειακή θερμοκρασία τους και με τρόπο ώστε να υπάρχει συνεχής μεταβολή των γραμμών απορρόϕησης από τύπο σε τύπο (ταξινόμηση του Harvard). Οι ϕασματικοί τύποι, από τους θερμότερους προς τους ψυχρότερους, είναι οι εξής. O. Επιϕανειακές θερμοκρασίες μεγαλύτερες των K και έως K. Φαινόμενο χρώμα κυανό. Γραμμές απορρόϕησης ιονισμένου ηλίου, αζώτου, πυριτίου, ασθενείς υδρογόνου. B. Επιϕανειακές θερμοκρασίες μεταξύ και K. Φαινόμενο χρώμα κυανό. Γραμμές απορρόϕησης ουδέτερου ηλίου, πυριτίου, οξυγόνου, μαγνησίου, έντονες υδρογόνου. A. Επιϕανειακές θερμοκρασίες μεταξύ 7500 και K. Φαινόμενο χρώμα κυανό προς κυανόλευκο. Γραμμές απορρόϕησης ισχυρές υδρογόνου, ιονισμένου
21 2.6 Το διάγραμμα Hertzsprung Russell 20 μαγνησίου, πυριτίου, σιδήρου, τιτανίου, ασβεστίου. F. Επιϕανειακές θερμοκρασίες μεταξύ 6000 και 7500 K. Φαινόμενο χρώμα κυανόλευκο προς λευκό. Γραμμές απορρόϕησης υδρογόνου, ιονισμένου ασβεστίου, σιδήρου, χρωμίου, και άλλων μετάλλων. G. Επιϕανειακές θερμοκρασίες μεταξύ 5000 και 6000 K. Φαινόμενο χρώμα κιτρινόλευκο προς κίτρινο. Γραμμές απορρόϕησης ιονισμένου ασβεστίου, μετάλλων, ασθενείς υδρογόνου, μοριακές ταινίες. K. Επιϕανειακές θερμοκρασίες μεταξύ 3500 και 5000 K. Φαινόμενο χρώμα πορτοκαλί προς ερυθρό. Γραμμές απορρόϕησης ουδέτερων μετάλλων, μοριακές ταινίες. M. Επιϕανειακές θερμοκρασίες μικρότερες των 3500 K. Φαινόμενο χρώμα ερυθρό. Γραμμές απορρόϕησης ουδέτερων μετάλλων, μοριακές ταινίες. Κάθε ένας από τους ϕασματικούς τύπους υποδιαιρείται σε 10 επιμέρους τύπους. Π.χ., ο ϕασματικός τύπος B υποδιαιρείται στους B0, B1, B2, B3, B4, B5, B6, B7, B8, και B9. Για τον ϕασματικό τύπο O, συνηθίζεται να δίνονται οι επιμέρους τύποι O5, O6, O7, O8, και O9. Στη βιβλιογραϕία, οι ϕασματικοί τύποι O και B αναϕέρονται συχνά ως «προγενέστεροι ϕασματικοί τύποι», ενώ οι ϕασματικοί τύποι K και M ως «μεταγενέστεροι ϕασματικοί τύποι». 2.6 To diˆgramma Hertzsprung Russell Η προσπάθεια γραϕικής συσχέτισης των δύο πιο σημαντικών ιδιοτήτων των αστέρων, δηλαδή των ϕασματικών τύπων (ή, ισοδύναμα, των επιϕανειακών θερμοκρασιών) με τα απόλυτα μεγέθη (ή, ισοδύναμα, με τις ϕωτεινότητες), οδήγησε σε ένα εξαιρετικά ενδιαϕέρον διάγραμμα. Το διάγραμμα αυτό είναι καρπός των ανεξάρτητων ερευνών δύο αστρονόμων. Συγκεκριμένα, το 1911, ο Δανός αστρονόμος Ejnar Hertzsprung μελέτησε το διάγραμμα θέτοντας στον οριζόντιο άξονα τις επιϕανειακές θερμοκρασίες (τετμημένες) και στον κάθετο άξονα τα απόλυτα μεγέθη (τεταγμένες). Το 1913, ο Αμερικανός αστρονόμος Henry Norris Russell έθεσε στον οριζόντιο άξονα τους ϕασματικούς τύπους, που παριστάνουν και αυτοί ένα μέτρο της επιϕανειακής θερμοκρασίας των αστέρων. Προς τιμήν των αστρονόμων αυτών, κάθε διάγραμμα αυτού του είδους αναϕέρεται σήμερα ως διάγραμμα Hertzsprung Russell ή ως διάγραμμα H R. Το Σχήμα 2.4 παριστάνει ένα τυπικό διάγραμμα H R. Ο οριζόντιος άξονας έχει βαθμονομηθεί σε ϕασματικούς τύπους (κάτω) και σε επιϕανειακές θερμοκρασίες (επάνω). Συγκεκριμένα, από την περιγραϕή των ϕασματικών τύπων στην 2.5, προκύπτουν οι αντιστοιχίες O K, B K, A K, F K, G K, K K, και M K. Ο κάθετος άξονας του διαγράμματος έχει βαθμονομηθεί σε απόλυτα μεγέθη στην αριστερή πλευρά και σε ϕωτεινότητες μετρούμενες με μονάδα μέτρησης την ηλιακή ϕωτεινότητα (Εξ. 2.12), L, στη δεξιά πλευρά. Η μετατροπή των απολύτων μεγεθών σε ϕωτεινότητες γίνεται εύκολα, επειδή το απόλυτο μέγεθος +5 αντιστοιχεί με ικανοποιητική προσέγγιση στον Ηλιο (Εξ. 2.11) που έχει ϕωτεινότητα L (= 1). Συγχρόνως, σε κάθε μείωση των απολύτων μεγεθών κατά 5 (δηλαδή από το +10 στο +5, από το +5 στο 0, από το 0 στο 5, από το 5 στο 10, κ.ο.κ) αντιστοιχεί αύξηση της ϕωτεινότητας κατά 100 ϕορές (Εξς. 2.2, 2.20 για δύο αστέρες σε απόσταση 10 pc και με απόλυτα μεγέθη M και N τέτοια ώστε N M = 5, ισχύει B M BN = 100 = L M LN ). Το διάγραμμα H R δείχνει ότι οι περισσότεροι αστέρες βρίσκονται στην κύρια
22 2.6 Το διάγραμμα Hertzsprung Russell 21 Σχήμα 2.4: Το διάγραμμα H R. ακολουθία (main sequence), δηλαδή σε μία στενή ζώνη που διασχίζει σχεδόν διαγώνια το διάγραμμα, από τον ϕασματικό τύπο O μέχρι τον M. Ο Ηλιος, με χρώμα κιτρινόλευκο προς κίτρινο, βρίσκεται περίπου στο μέσο της κύριας ακολουθίας. Από τον ϕασματικό τύπο F μέχρι τον M, διακλαδίζεται από την κύρια ακολουθία ένας δεύτερος κλάδος, επί του οποίου βρίσκονται οι γίγαντες αστέρες (giant sars). Οι αστέρες αυτοί έχουν σχετικά χαμηλές επιϕανειακές θερμοκρασίες, αλλά μεγαλύτερες ϕωτεινότητες από τους αντίστοιχους ισόθερμους αστέρες της κύριας ακολουθίας. Πρέπει λοιπόν να έχουν μεγαλύτερες ακτίνες από αυτούς, δηλαδή να είναι γίγαντες σε σύγκριση με αυτούς. Πράγματι, έστω ότι ένας αστέρας στην περιοχή των γιγάντων έχει ϕασματικό τύπο K0 και ϕωτεινότητα L G εκατονταπλάσια της ϕωτεινότητας L M ενός αστέρα της κύριας ακολουθίας, ίδιου ϕασματικού τύπου. Άν συμβολίσουμε με R G, R M τις ακτίνες των αστέρων αυτών και με T την κοινή επιϕανειακή θερμοκρασία τους, τότε ισχύει (Εξς. 1.17, 1.18, 1.22) L G = 4 π R2 G σ T 4 L M 4 π RM 2 σ T 4 = R2 G. (2.28) Λύνοντας την εξίσωση αυτήν ως προς την ακτίνα R G του γίγαντα αστέρα, βρί- R 2 M
23 2.7 Παραγωγή ενέργειας στους αστέρες 22 σκουμε R G = R M LG L M = 10 R M. (2.29) Ωστε ο γίγαντας αστέρας του παραδείγματός μας έχει ακτίνα δεκαπλάσια του αντίστοιχου αστέρα της κύριας ακολουθίας. Επάνω από την περιοχή των γιγάντων αστέρων, βρίσκονται και άλλοι αστέρες με περίπου ίδιους ϕασματικούς τύπους, αλλά με πολύ μεγαλύτερες ϕωτεινότητες από τους αντίστοιχους αστέρες της κύριας ακολουθίας. Ιδιοι συλλογισμοί με αυτούς του προηγούμενου παραδείγματος, οδηγούν στο συμπέρασμα ότι οι αστέρες αυτοί έχουν πολύ μεγαλύτερες ακτίνες από τους αντίστοιχους αστέρες της κύριας ακολουθίας. Ονομάζονται λοιπόν υπεργίγαντες αστέρες (supergiant stars). Στην κάτω αριστερή περιοχή του διαγράμματος H R υπάρχει μία σχετικά απομονωμένη ομάδα αστέρων, οι οποίοι έχουν υψηλές επιϕανειακές θερμοκρασίες, με χρώματα από κυανό μέχρι κίτρινο (συνήθως λευκό σπανιότατα ερυθρό). Ομως οι ϕωτεινότητές τους είναι μικρές σε σύγκριση με τους αντίστοιχους αστέρες της κύριας ακολουθίας. Συνεπώς οι αστέρες αυτοί έχουν μικρές ακτίνες σε σύγκριση με τους αντίστοιχους αστέρες της κύριας ακολουθίας. Από το (συνήθως) λευκό χρώμα τους και από το μικρό μέγεθός τους, έχουν πάρει το όνομα λευκοί νάνοι (white dwarfs). Πάντως και οι αστέρες της κύριας ακολουθίας με απόλυτο μέγεθος μικρότερο του +5, συνηθίζεται να χαρακτηρίζονται ως νάνοι αστέρες (dwarf stars). Ομως οι νάνοι αστέρες της κύριας ακολουθίας έχουν χρώματα από κίτρινο μέχρι ερυθρό και, έτσι, διαϕοροποιούνται από τους λευκούς νάνους. 2.7 Paragwg enèrgeiac stouc astèrec Purhnik sônthxh Ο κύριος μηχανισμός παραγωγής ενέργειας στους αστέρες είναι η πυρηνική σύντηξη (nuclear fusion) του υδρογόνου και βαρύτερων στοιχείων. Ενας άλλος μηχανισμός παραγωγής ενέργειας είναι η βαρυτική συστολή (gravitational contraction), όπου μέρος της βαρυτικής δυναμικής ενέργειας ενός αστέρα μετατρέπεται σε θερμότητα. Η σύντηξη του υδρογόνου συμβαίνει σε θερμοκρασίες 10 7 K, όπου δύο πυρήνες υδρογόνου, δηλαδή δύο πρωτόνια, έχουν αρκετή κινητική ενέργεια για να υπερνικήσουν τη μεταξύ τους ηλεκτρική άπωση και να εμπλακούν στον λεγόμενο «κύκλο πρωτονίου πρωτονίου» (proton proton chain). Συγκεκριμένα, δύο πρωτόνια συγκρούονται μεταξύ τους και παράγουν έναν πυρήνα δευτερίου (= βαρύ υδρογόνο), ένα ποζιτρόνιο (= ηλεκτρόνιο θετικού ϕορτίου, αντιύλη του ηλεκτρονίου), και ένα νετρίνο (= ουδέτερο σωμάτιο εξαιρετικά μικρής μάζας ηρεμίας κινούμενο με ταχύτητα παραπλήσια του ϕωτός). Στη συνέχεια, το δευτέριο συγκρούεται με ένα πρωτόνιο παράγοντας έναν ελαϕρύ πυρήνα ηλίου (= δύο πρωτόνια και ένα νετρόνιο) και ένα ϕωτόνιο στην περιοχή των ακτίνων γ (Σχ. 1.3). Επειτα, δύο ελαϕροί πυρήνες ηλίου συγκρούονται μεταξύ τους παράγοντας έναν πυρήνα ηλίου (= δύο πρωτόνια και δύο νετρόνια) και δύο πρωτόνια, τα οποία μπορούν να ξανασυμμετάσχουν στον κύκλο. Η μάζα του πρωτονίου, m p, είναι m p = kg. (2.30)
24 2.7 Παραγωγή ενέργειας στους αστέρες 23 Στην πυρηνική αντίδραση εμπλέκονται έξι πρωτόνια με συνολική μάζα kg. Αϕού η μάζα ενός πυρήνα ηλίου, m He, είναι m He = kg, (2.31) τα προϊόντα της πυρηνικής αντίδρασης, δηλαδή ένας πυρήνας ηλίου και δύο πρωτόνια, έχουν συνολική μάζα kg. Ωστε στην πυρηνική αντίδραση του κύκλου πρωτονίου πρωτονίου προκύπτει έλλειμα μάζας m pp = kg, το οποίο μετατρέπεται σε ενέργεια σύμϕωνα με τη σχέση μάζας ενέργειας του Einstein, E pp = m pp c 2 = J. (2.32) Συνεπώς ο αριθμός πυρηνικών αντιδράσεων του κύκλου πρωτονίου πρωτονίου που λαμβάνουν χώρα ανά δευτερόλεπτο, N pp, είναι N pp = L E pp = s 1. (2.33) Αυτό σημαίνει ότι το έλλειμα μάζας ανά δευτερόλεπτο, Mpp t, ανέρχεται σε M pp t = N pp m pp = kg s 1. (2.34) Ως επαλήθευση των προηγούμενων πράξεων, υπολογίζουμε το έλλειμα μάζας ανά δευτερόλεπτο απευθείας από τη σχέση μαζας ενέργειας του Einstein, M pp t = L c 2 = kg s 1. (2.35) Ωστε κάθε δευτερόλεπτο 4.5 εκατομμύρια τόννοι ηλιακής μάζας μετατρέπονται σε ενέργεια. Σε σύγκριση με τη μάζα του Ηλιου, M = kg = tons, (2.36) η ποσότητα Mpp t είναι πολύ μικρή. Υπολογίζεται ότι το υδρογόνο του Ηλιου είναι αρκετό για να συνεχισθεί η παραγωγή ενέργειας επί 5 δισεκατομμύρια έτη, δηλαδή επί όσον ακόμη χρόνο θα παραμείνει ο Ηλιος στην κύρια ακολουθία. Σε αστέρες αρκετά μεγαλύτερης μάζας από αυτήν του Ηλιου, η πυρηνική σύντηξη επιτυγχάνεται με τον «κύκλο του άνθρακα». Ο άνθρακας συμμετέχει ως καταλύτης στον κύκλο αυτόν, μετατρεπόμενος διαδοχικά σε άζωτο, οξυγόνο, και πάλι σε άνθρακα. Εμπλέκονται όμως και 4 πυρήνες υδρογόνου, αποϕέροντας ως καθαρό προϊόν της αντίδρασης αυτής έναν πυρήνα ηλίου, δύο ποζιτρόνια και ηλεκτρομαγνητική ακτινοβολία στην περιοχή των ακτίνων γ. Η «θερμοκρασία ανάϕλεξης» για τη θερμοπυρηνική καύση του υδρογόνου είναι 10 7 K. Βαρύτερα στοιχεία χρειάζονται μεγαλύτερες θερμοκρασίες για να υποστούν πυρηνική σύντηξη. Π.χ, το ήλιο έχει θερμοκρασία ανάϕλεξης K και ο άνθρακας K Barutik sustol Η «βαρυτική δυναμική ενέργεια», W, ενός αστέρα μάζας M και ακτίνας R υπολογίζεται προσεγγιστικά από τον τύπο W = 3 G M 2 5 R. (2.37)
25 2.8 Οι αστέρες ως ενεργειακές μηχανές 24 Άν η ακτίνα του αστέρα συσταλεί σε ένα κλάσμα της αρχικής, ξr, τότε ο αστέρας θα αποδεσμεύσει ενέργεια υπό μορϕή θερμότητας, E W, ίση με E W = 3 G M 2 5 R ( 3 G M 2 ) = 3 G M 2 5 ξ R 5 R ( ) 1 ξ 1. (2.38) Π.χ., άν η ακτίνα του Ηλιου συσταλεί σε ξ R = 0.9 R, τότε θα αποδεσμευθεί υπό μορϕή θερμότητας ενέργεια ίση με E W = ( ) = J (2.39) Η ενέργεια αυτή θα μπορούσε να αποτελεί την πηγή ϕωτεινότητας του Ηλιου για χρονικό διάστημα E W L y. Η παραγωγή θερμότητας με τον μηχανισμό της βαρυτικής συστολής είναι σημαντική στο πρώτο στάδιο της ζωής ενός αστέρα, δηλαδή όταν αυτός είναι «πρωτοαστέρας» (= αστρικό έμβρυο). Τότε έχει πολύ μεγάλη ακτίνα, πολύ μικρή πυκνότητα, και πολύ χαμηλή θερμοκρασία. Ως πρωτοαστέρας, ο Ηλιος είχε ακτίνα περίπου ίση με την ακτίνα της τροχιάς του Πλούτωνα, R 40 AU = m. Επαναλαμβάνοντας τους συλλογισμούς του προηγούμενου παραδείγματος και εκτελώντας τις πράξεις, βρίσκουμε ότι, άν μοναδική πηγή ενέργειας του Ηλιου ήταν η βαρυτική συστολή του, τότε η ενεργειακή ηλικία του δεν θα μπορούσε να υπερβεί τα 30 εκατομμύρια έτη. Σε αντιδιαστολή με αυτή τη σύντομη χρονική περίοδο, ο μηχανισμός πυρηνικής σύντηξης αποϕέρει μία εξαιρετικά μακρά χρονική περίοδο παραγωγής ενέργειας με σταθερή ισχύ, ίση προς την παρατηρούμενη σήμερα ϕωτεινότητα του Ηλιου. Οταν η βαρυτική συστολή λαμβάνει χώρα με έντονο ρυθμό, τότε λέμε ότι ο αστέρας υπόκειται σε «βαρυτική κατάρρευση» (gravitational collapse). 2.8 Oi astèrec wc energeiakèc mhqanèc Ο τρόπος με τον οποίο διαμορϕώνεται ένας αστέρας, για να λειτουργήσει ως ενεργειακή μηχανη, εξαρτάται από τη μάζα του. Διακρίνουμε τις ακόλουθες περιπτώσεις. 1. Αστέρας με μάζα μικρότερη του 0.8M. Οι θερμοπυρηνικές αντιδράσεις γίνονται στον κεντρικό «πυρήνα» του αστέρα, όπου και παράγεται η ενέργεια. Αυτός περιβάλλεται από μία «ζώνη μεταϕοράς» που εκτείνεται μέχρι την επιϕάνεια. Στη ζώνη μεταϕοράς, η προς τα έξω διάδοση της παραγόμενης στον πυρήνα ενέργειας γίνεται με μεταϕορά μάζας. 2. Αστέρας με μάζα μεταξύ 0.8M και 4M. Οι θερμοπυρηνικές αντιδράσεις και η παραγωγή ενέργειας λαμβάνουν χώρα στον πυρήνα του αστέρα. Αυτός έχει ακτίνα 0.25R (όπου R η ακτίνα του αστέρα). Ο πυρήνας περιβάλλεται από τη «ζώνη ακτινοβολίας», που εκτείνεται μέχρι 0.70R. Στη ζώνη αυτή, η ενέργεια διαδίδεται με ακτινοβολία. Το εσωτερικό του αστέρα, δηλαδή ο πυρήνας και η ζώνη ακτινοβολίας, περιβάλλεται από τη «ζώνη μεταϕοράς» που εκτείνεται μέχρι την επιϕάνεια. Στη ζώνη μεταϕοράς, η διάδοση της ενέργειας γίνεται με μεταϕορά μάζας. 3. Αστέρας με μάζα μεγαλύτερη του 4M. Εδώ ο αστέρας διαμορ- ϕώνεται κατά τρόπο αντίστροϕο της δεύτερης περίπτωσης. Συγκεκριμένα, ο πυρήνας περιβάλλεται από μία «ζώνη μεταϕοράς», στην οποία η ενέργεια διαδίδεται με
26 2.9 Ιδιότητες των αστέρων της κύριας ακολουθίας 25 μεταϕορά μάζας. Ακολουθεί μία «ζώνη ακτινοβολίας» που εκτείνεται μέχρι την επιϕάνεια. Στη ζώνη αυτή, η διάδοση της ενέργειας γίνεται με ακτινοβολία. Στον πυρήνα ενός αστέρα επικρατούν εξαιρετικά υψηλές θερμοκρασίες (για τον Ηλιο, π.χ., K). Συνεπώς ο ιονισμός των ατόμων είναι πλήρης. Αυτό σημαίνει ότι στον αστρικό πυρήνα υπάρχουν μόνο γυμνοί ατομικοί πυρήνες και ηλεκτρόνια (= πλάσμα). Ως ενεργειακές μηχανές, οι αστέρες προσπαθούν να επιτύχουν «θερμική ισορροπία» και «υδροστατική ισορροπία». Η θερμική ισορροπία αϕορά το ισοζύγιο παραγόμενης εκπεμπόμενης ενέργειας. Άν η εκπεμπόμενη ενέργεια είναι λιγότερη της παραγόμενης, τότε στο εσωτερικό του αστέρα εγκλωβίζεται θερμότητα και η θερμοκρασία αυξάνεται. Για να διαϕύγει η συσσωρευόμενη θερμότητα, οδηγεί τον αστέρα σε εκρηκτικά ϕαινόμενα. Άν πάλι η εκπεμπόμενη ενέργεια είναι περισσότερη της παραγόμενης, τότε η θερμοκρασία του αστέρα μειώνεται συνεχώς, επειδή αποβάλλεται από τον αστέρα θερμότητα που δεν αναπληρώνεται. Η υδροστατική ισορροπία αϕορά το ισοζύγιο πίεσης βαρύτητας. Ενας αστέρας πρέπει να παράγει τόση ενέργεια, ώστε η θερμοκρασία του να δίνει, συμϕωνα με την καταστατική εξίσωση των ιδανικών αερίων (Εξ. 1.14), τη σωστή εσωτερική πίεση για την επίτευξη του ισοζύγιου πίεσης βαρύτητας. Υψηλότερη πίεση στο εσωτερικό του αστέρα αντιστοιχεί σε δυνάμεις που επικρατούν της βαρυτικής έλξης και ο αστέρας οδηγείται σε διαστολή. Χαμηλότερη πίεση αντιστοιχεί σε δυνάμεις που υπερνικώνται από τη βαρυτική έλξη και ο αστέρας οδηγείται σε συστολή. Εκτός από την πίεση που επάγεται από τη θερμοκρασία των αερίων του αστέρα, στο ισοζύγιο πίεσης βαρύτητας συνεισϕέρει και η «πίεση ακτινοβολίας», δηλαδή η πίεση που επάγεται από τις συγκρούσεις των προς τα έξω κινούμενων ϕωτονίων με την ύλη του αστέρα. 2.9 Idiìthtec twn astèrwn thc kôriac akoloujðac Οι αστέρες της κύριας ακολουθίας έχουν επιτύχει θερμική και υδροστατική ισορροπία. Παράγουν στον πυρήνα τους ενέργεια με σταθερό ρυθμό, η οποία διατηρεί σταθερή την κατανομή της θερμοκρασίας στο εσωτερικό τους. Η θερμοκρασιακή αυτή κατανομή εξασϕαλίζει τη διαρκή εξισορρόπηση των προς τα έξω δυνάμεων της πίεσης με τις προς τα μέσα δυνάμεις της βαρύτητας. Η παραγόμενη ενέργεια διαδίδεται με ακτινοβολία μέσα από τη ζώνη ακτινοβολίας και με μεταϕορά μέσα από τη ζώνη μεταϕοράς, μέχρι την αστρική επιϕάνεια, όπου και αποβάλλεται υπό μορϕή ηλεκτρομαγνητικής ακτινοβολίας μέλανος σώματος. Τον ρόλο του μέλανος σώματος έχει η «ϕωτόσϕαιρα». Αυτή αποτελείται από τα πλέον εξωτερικά αέρια στρώματα του αστέρα, έχει πολύ μικρό πάχος (π.χ., για τον Ηλιο 400 km), και αποτελεί ζώνη ακτινοβολίας με συμπεριϕορά μέλανος σώματος. Στην κύρια ακολουθία, οι αστέρες μεγαλύτερης μάζας έχουν μεγαλύτερες ακτίνες σε σύγκριση με τους αστέρες μικρότερης μάζας. Αυτή ακριβώς η συμπεριϕορά ευθύνεται για τη λεγόμενη «σχέση μάζας ϕωτεινότητας». Συγκεκριμένα, μεγαλύτερη μάζα σημαίνει ισχυρότερη βαρύτητα. Για να εξισορροπηθεί αυτή, χρειάζεται υψηλότερη θερμοκρασία και πίεση, οπότε ο αντίστοιχος αστέρας καίει με ταχύτερο ρυθμό το υδρογόνο στον πυρήνα του. Επειδή είναι θερμότερος και έχει μεγαλύτερη ακτίνα, ο αστέρας αυτός έχει μεγαλύτερη ϕωτεινότητα σε σύγκριση με έναν άλλο αστέρα μικρότερης μάζας. Οι συλλογισμοί αυτοί οδηγούν στη σχέση μάζας
27 2.10 Η εξέλιξη των αστέρων 26 ϕωτεινότητας για τους αστέρες της κύριας ακολουθίας, η οποία διατυπώνεται, σύμϕωνα με τις παρατηρήσεις, ως ( ) ( ) L M log = 3.5 log, (2.40) L όπου L και M είναι η ϕωτεινότητα και η μάζα ενός αστέρα της κύριας ακολουθίας. Στην κύρια ακολουθία, ένας αστέρας μεγαλύτερης μάζας υποχρεώνεται να καίει με ταχύτερο ρυθμό το υδρογόνο στον πυρήνα του, ώστε να βρίσκεται διαρκώς σε θερμική και υδροστατική ισορροπία. Ο χρόνος παραμονής του αστέρα στην κύρια ακολουθία λήγει με την εξάντληση του υδρογόνου στον πυρήνα. Συνεπώς ένας αστέρας μεγαλύτερης μάζας παραμένει στην κύρια ακολουθία λιγότερο από έναν αστέρα μικρότερης μάζας. Η παρατήρηση δείχνει ότι ισχύει η ακόλουθη «σχέση μάζας χρόνου παραμονής για τους αστέρες της κύριας ακολουθίας» ( ) ( ) t M log = 2.5 log, (2.41) t M M όπου t είναι ο χρόνος παραμονής ενός αστέρα μάζας M και t y (2.42) είναι ο εκτιμώμενος χρόνος παραμονής του Ηλιου στην κύρια ακολουθία H exèlixh twn astèrwn Στην εξέλιξη των αστέρων διακρίνουμε τρεις ϕάσεις, με διαϕορετική διάρκεια η κάθε μία. 1. Πρώτη ϕάση. Αυτή περιλαμβάνει τη γέννηση ενός αστέρα, δηλαδή την εμϕάνιση ενός μορϕώματος που ονομάζεται πρωτοαστέρας, και την εξέλιξή του μέχρι την κύρια ακολουθία. Η πρώτη ϕάση έχει πολύ σύντομη διάρκεια σε σύγκριση με τη συνολική διάρκεια ζωής του αστέρα. 2. Δεύτερη ϕάση. Αϕορά την παραμονή του αστέρα στην κύρια ακολουθία. Εκεί βρίσκεται υπό συνθήκες θερμικής και υδροστατικής ισορροπίας ( 2.9) χρησιμοποιώντας ως θερμοπυρηνικό καύσιμο το υδρογόνο του πυρήνα του ( 2.7.1). Η ϕάση αυτή διαρκεί πολύ περισσότερο από τις άλλες δύο. 3. Τρίτη ϕάση. Οταν εξαντληθεί το υδρογόνο στον πυρήνα του αστέρα, αυτός επιχειρεί να εξισορροπήσει τη βαρύτητα καίγοντας βαρύτερα θερμοπυρηνικά καύσιμα, όπως το ήλιο, ο άνθρακας, το οξυγόνο, κ.λπ. Συμπληρωματικά, χρησιμοποιεί για την παραγωγή ενέργειας και τον μηχανισμό της βαρυτικής συστολής ( 2.7.2). Στη ϕάση αυτή, ο αστέρας μπορεί να εξελιχθεί σε γίγαντα ή και υπεργίγαντα. Οταν εξαντληθούν όλες οι διαθέσιμες πηγές ενέργειας, ο αστέρας γίνεται, ανάλογα με τη μάζα του, «λευκός νάνος», «αστέρας νετρονίων», ή «μελανή οπή». Στη βιβλιογραϕία, συνηθίζεται να αναϕέρονται αυτές οι τρεις τελικές καταστάσεις ενός αστέρα ως «αστρικά πτώματα». Η τρίτη ϕάση διαρκεί πολύ λίγο σε σύγκριση με τη δεύτερη ϕάση.
28 2.11 Εξέλιξη αστέρων με απομένουσα μάζα 1.4M : λευκοί νάνοι Exèlixh astèrwn me apomènousa mˆza 1.4M : leukoð nˆnoi Μετά την απομάκρυνση των εξωτερικών στρωμάτων, στον αστέρα απομένει μόνον ο πυρήνας του. Άν η απομένουσα μάζα είναι μικρότερη ή ίση του λεγόμενου «ορίου Chandrasekhar», M Ch, που είναι M Ch = 1.4 M, (2.43) τότε ο αστέρας δεν θα ϕτάσει ποτέ τη θερμοκρασία ανάϕλεξης για την καύση του άνθρακα στον πυρήνα του ( 2.7.1). Χωρίς παραγωγή ενέργειας, οδηγείται από τη βαρυτική συστολή σε μία κατάσταση με πυκνότητες 10 6 g cm 3. Η κατάσταση αυτή είναι πανομοιότυπη με εκείνη που επικρατούσε στον πυρήνα του αστέρα ελάχιστα πριν από την εκδήλωση του ϕλας ηλίου. Συγκεκριμένα, το αέριο των ελευθέρων ηλεκτρονίων είναι εκϕυλισμένο. Δεν περιγράϕεται από την κινητική θεωρία των ιδανικών αεριών ( 1.2) και οι ταχύτητες των ηλεκτρονίων δεν ακολουθούν τη στατιστική Maxwell Boltzmann. Αντί αυτής, ακολουθούν τη στατιστική Fermi Dirac, η οποία προκύπτει από τους νόμους της κβαντομηχανικής. Το βασικό χαρακτηριστικό αυτής της εκϕυλισμένης ύλης είναι ότι τα ηλεκτρόνια κινούνται ελεύθερα ως αέριο ελευθέρων ηλεκτρονίων, μέσα στο οποίο παραμένουν εμβαπτισμένοι οι ατομικοί πυρήνες. Σύμϕωνα με τη στατιστική Fermi Dirac, το αέριο των ελευθέρων ηλεκτρονίων ασκεί πίεση στο περιβάλλον του, η οποία δεν είναι θερμικής προέλευσης, δηλαδή δεν είναι συνάρτηση της θερμοκρασίας. Συνεπώς η πίεση αυτή υπάρχει ακόμη και όταν δεν παράγεται ενέργεια για να διατηρήσει τον αστέρα θερμό. Η προηγούμενη κατάσταση με την ύπαρξη εκϕυλισμένης ύλης στον πυρήνα του αστέρα ήταν προσωρινή, αϕού έπαυε να ισχύει αμέσως μετά την εκδήλωση του ϕλας ηλίου. Ομως τώρα δεν υπάρχει ήλιο για να εκδηλωθεί ένα νέο ϕλας ηλίου και η παρούσα κατάσταση με την ύπαρξη εκϕυλισμένης ύλης μονιμοποιείται. Στη μορϕή αυτή, ο αστέρας ονομάζεται λευκός νάνος (white dwarf). Αποτελείται κυρίως από άνθρακα με κρυσταλλική δομή. Δεν έχει μηχανισμούς παραγωγής ενέργειας στο εσωτερικό του. Διαθέτει μόνον εσωτερική ενέργεια και περιστροϕική κινητική ενέργεια. Εκπέμπει ηλεκτρομαγνητική ακτινοβολία σε βάρος των ενεργειακών αποθεμάτων του. Συνεπώς ψύχεται σταδιακά και καταλήγει μετά από μακρό χρόνο σε έναν «μελανό νάνο». Η θεωρία των λευκών νάνων αναπτύχθηκε κυρίως από τον διάσημο Ινδό α- στροϕυσικό Subrahmanyan Chandrasekhar στις αρχές της δεκαετίας του Ο Ηλιος θα τερματίσει τη ζωή του ως λευκός νάνος. Αυτό αναμένεται να γίνει σε y. Τότε θα έχει ακτίνα περίπου ίση με την ακτίνα της Γης (ένας τυπικός λευκός νάνος έχει ακτίνα 10 4 km, δηλαδή R ) Exèlixh astèrwn me apomènousa mˆza metaxô 1.4M kai 3.2M : astèrec netronðwn Άν για την απομένουσα μάζα του αστέρα, M, ισχύει η σχέση M Ch < M < M LOV, όπου M Ch είναι το όριο Chandrasekhar (Εξ. 2.43) και M LOV = 3.2 M (2.44)
29 2.13 Εξέλιξη αστέρων με απομένουσα μάζα >3.2M : μελανές οπές 28 είναι το λεγόμενο «όριο Landau Oppenheimer Volkoff», τότε ο αστέρας γίνεται αστέρας νετρονίων (neutron star), δηλαδή αποτελείται σχεδόν αποκλειστικά από νετρόνια. Αυτό συμβαίνει για τους εξής λόγους. Η ύλη του υπολείμματος συμπιέζεται λόγω βαρυτικής συστολής και η πυκνότητά του ϕτάνει τα 10 9 g cm 3. Τότε τα εκϕυλισμένα ελεύθερα ηλεκτρόνια αποκτούν, σύμϕωνα με τη στατιστική Fermi Dirac, πολύ μεγάλες ταχύτητες και κινητικές ενέργειες. Ενα τέτοιο υπερενεργητικό ηλεκτρόνιο και ένα πρωτόνιο, όταν συγκρούονται, δίνουν ένα νετρονιο και ένα ϕωτόνιο. Ετσι ο αριθμός των νετρονίων μεγαλώνει, ενώ ο αριθμός των ελευθέρων ηλεκτρονίων μικραίνει. Το αποτέλεσμα είναι να μειώνεται η πίεση του εκϕυλισμένου αερίου των ηλεκτρονίων και ο αστέρας να συστέλλεται περισσότερο. Αρχίζει να σχηματίζεται ένα «αέριο ελευθέρων νετρονίων», το οποίο συνυπάρχει με το αέριο των ελευθέρων ηλεκτρονίων και με πολλούς πυρήνες πλούσιους σε νετρόνια. Σε πυκνότητες g cm 3, το «αέριο των ελευθέρων νετρονίων» αρχίζει να συμπεριϕέρεται ως εκϕυλισμένη ύλη και η πίεση που ασκεί στο περιβάλλον του επιβραδύνει σημαντικά τη βαρυτική κατάρρευση. Ενώ σε πυκνότητες g cm 3, η πίεση του εκϕυλισμένου αερίου των ελευθέρων νετρονίων ανακόπτει πλήρως τη βαρυτική κατάρρευση. Ενας αστέρας νετρονίων έχει τυπική ακτίνα 10 km, και τυπική πυκνότητα στο κέντρο του g cm 3. Σύμϕωνα με την ορολογία που χρησιμοποιήθηκε και στους λευκούς νάνους ( 2.11), ο αστέρας νετρονίων αποτελεί ένα αστρικό πτώμα Exèlixh astèrwn me apomènousa mˆza >3.2M : melanèc opèc Οταν η απομένουσα μάζα του αστέρα είναι > 3.2 M, η πίεση του εκϕυλισμένου αερίου των ελευθέρων ηλεκτρονίων δεν μπορεί να ανακόψει τη βαρυτική κατάρρευση του αστέρα. Το αποτέλεσμα της πλήρους βαρυτικής κατάρρευσης είναι μία μελανή οπή (black hole). Στο πλαίσιο της Νευτώνειας μηχανικής, η μελανή οπή ορίζεται με ιδιαίτερα απλό τρόπο: είναι σώμα με μάζα M και ακτίνα R, τέτοιες ώστε η ταχύτητα διαϕυγής να προκύπτει μεγαλύτερη της ταχύτητας του ϕωτός. Συνεπώς, από μία μελανή οπή δεν μπορούν να διαϕύγουν ούτε καν τα ϕωτόνια TaqÔthta diafug c Σώμα μάζας m περιστρέϕεται γύρω από δεύτερο σώμα μάζας M, όπου m M για απλότητα, τα σώματα αυτά θα αναϕέρονται ως m και M. Στην περίπτωση που η ταχύτητα του m είναι πολύ μεγάλη, τότε αυτό θα δραπετεύσει οριστικά από τη βαρυτική έλξη του M, κινούμενο επί υπερβολικής τροχιάς. Τούτο θα συμβεί όταν η ταχύτητα γίνει μεγαλύτερη μίας οριακής τιμής, v, η οποία υπολογίζεται μέσω του έργου που απαιτείται για να μετακινηθεί το m από την επιϕάνεια του M (το οποίο θεωρείται σϕαιρικό με ακτίνα R M ) μέχρι του απείρου. Συγκεκριμένα, ισχύει η σχέση 1 2 mv2 = R M G M m r 2 dr = GM m, (2.45) R M
30 2.13 Εξέλιξη αστέρων με απομένουσα μάζα >3.2M : μελανές οπές 29 που, επιλυόμενη ως προς v, δίνει v = 2GM R M. (2.46) Η ταχύτητα v ονομάζεται ταχύτητα διαϕυγής. Για την περίπτωση της Γης, αυτή είναι ίση με 2 ( ) (6 10 v,e = 24 ) = m s 1 = 11.2 km s 1. (2.47) Άν η ταχύτητα του σώματος m είναι ακριβώς ίση με την ταχύτητα διαϕυγής, v, τότε αυτό θα απομακρυνθεί από το σώμα M διαγράϕοντας παραβολική τροχιά Fusikˆ qarakthristikˆ twn melan n op n Σε απλό Νευτώνειο μοντέλο μελανής οπής με μάζα M > 3.2 M, αρχικά υπολογίζεται η ακτίνα, R S, έτσι ώστε η ταχύτητα διαϕυγής από την επιϕάνεια (Εξ. 2.46), v, να είναι ίση με την ταχύτητα του ϕωτός, c, R S = 2 G M c 2. (2.48) Η ακτίνα αυτή λέγεται ακτίνα Schwarzschild της μελανής οπής. Τότε η μελανή οπή αρκεί να έχει μία ελάχιστα μικρότερη ακτίνα, για να μην μπορεί να διαϕύγει από αυτήν κανένα σωμάτιο. Η R S ορίζει μία επιϕάνεια που ονομάζεται ορίζοντας γεγονότων της μελανής οπής. Μπορεί να αποδειχθεί εύκολα ότι, με τη μάζα M μετρούμενη σε ηλιακές μάζες, M, και το μήκος σε km, η Εξίσωση 2.48 γράϕεται ( ) M R S 3 km. (2.49) Το 1972, ο Jacob Bekenstein ( ) διετύπωσε την υπόθεση ότι μία μελανή οπή έχει εντροπία, S, ανάλογη προς το εμβαδόν A = 4 π RS 2 του ορίζοντα γεγονότων. Σύμϕωνα με τη θερμοδυναμική, αϕού η μελανή οπή έχει εντροπία, έχει και θερμοκρασία, T, ανάλογη προς την επιϕανειακή της βαρύτητα. Η θερμοκρασία αυτή δίνεται από τη σχέση ( ) T = 10 7 M K. (2.50) M Ωστε η μελανή οπή συμπεριϕέρεται ως μέλαν σώμα ( και Σχ. 1.4), απορροϕώντας πλήρως τις ακτινοβολίες που προσπίπτουν σε αυτήν, αλλά και εκπέμποντας ακτινοβολία μέλανος σώματος όταν βρίσκεται σε ψυχρότερο από αυτήν περιβάλλον. Σύμϕωνα με τον νόμο μετατόπισης του Wien, το χαρακτηριστικό χρώμα, λ max, της μελανής οπής είναι αντιστρόϕως ανάλογο προς τη θερμοκρασία της (Εξ. 1.20), T. Με χρήση των Εξισώσεων 2.49 και 2.50, μπορεί να αποδειχθεί εύκολα ότι το χαρακτηριστικό χρώμα της μελανής οπής δίνεται από τη σχέση M λ max 10 R S. (2.51) Στη βιβλιογραϕία απαντάται και η σχέση λ max 2πR S που αποδίδει έμϕαση στο γεγονός ότι το χαρακτηριστικό χρώμα είναι της τάξης μεγέθους του μήκους της περιϕέρειας του ορίζοντα γεγονότων.
31 2.14 Μεταβλητοί αστέρες 30 Η θερμοδυναμική συμπεριϕορά των μελανών οπών βρίσκεται σε διάσταση με τον κλασικό ορισμό τους, σύμϕωνα με τον οποίο δεν μπορούν να διαϕύγουν από αυτές ούτε καν τα ϕωτόνια. Το δύσκολο αυτό πρόβλημα λύθηκε από τον Stephen Hawking, ο οποίος θεμελίωσε την «κβαντομηχανική των μελανών οπών». Η «αρχή της απροσδιοριστίας του Heisenberg» και το «ϕαινόμενο της σήραγγας» μπορούν να δώσουν μία απλουστευμένη περιγραϕή αυτού του μηχανισμού, ο οποίος αναϕέρεται στη βιβλιογραϕία ως μηχανισμός ή εκπομπή ή ϕαινόμενο Hawking, αλλά η αυστηρή ερμηνεία του απαιτεί πρόσθετη ανάλυση που εκϕεύγει του πλαισίου της παρούσας περιληπτικής διαπραγμάτευσης. Ο μηχανισμός Hawking οδηγεί τη μελανή οπή σε απώλεια μάζας με αποτέλεσμα να αυξάνεται η θερμοκρασία της (Εξ. 2.50) και να επιταχύνεται η εκπομπή ϕωτονίων και σωματίων. Οταν πλησιάζει η πλήρης εξάντληση της μάζας της, η μελανή οπή αναδύεται στον χώρο υπό συνθήκες ισχυρότατης έκρηξης σε αυτή την τελική εκρηκτική ϕάση, χαρακτηριστική είναι η εκπομπή ακτίνων γ υψηλής ενέργειας. Ως «χρόνος εξάχνωσης», t e, αναϕέρεται η συνολική διάρκεια του ϕαινομένου. Ο χρόνος αυτός δίνεται από τη σχέση ( ) 3 M t e = y. (2.52) M Οι Εξισώσεις 2.50 και 2.52 δείχνουν ότι ο μηχανισμός Hawking αποκτά μεγάλο ενδιαϕέρον για μελανές οπές που δεν έχουν προκύψει από την εξέλιξη αστέρων, δηλαδή που δεν έχουν μάζες > 3.2 M, αλλά που (ενδεχομένως) έχουν δημιουργηθεί κατά την αρχική ϕάση της εξέλιξης του Σύμπαντος. Αυτές (εϕόσον υπάρχουν, θα) είναι μικρές μελανές οπές με μάζες kg αναϕέρονται στη βιβλιογραϕία ως αρχέγονες μελανές οπές. Λόγω της μικρής μάζας τους, έχουν θερμοκρασίες K και χρόνους εξάχνωσης y, δηλαδή συγκρίσιμους με την ηλικία του Σύμπαντος MetablhtoÐ astèrec Η παρατήρηση δείχνει ότι υπάρχουν αστέρες μεταβαλλόμενης λαμπρότητας. Οι αστέρες αυτοί ονομάζονται μεταβλητοί αστέρες (variable stars). Ενας από τους πιο γνωστούς μεταβλητούς αστέρες είναι ο αστέρας o του Κήτους (o Cet: Mira, Mirabilis), για τον οποίο ο Fabricius διαπίστωσε το 1596 ότι υπόκειται σε περιοδική μεταβολή της λαμπρότητάς του. Οι μεταβλητοί αστέρες διακρίνονται στους «περιοδικούς μεταβλητούς» και στους «μή περιοδικούς μεταβλητούς». Οι περιοδικοί μεταβλητοί διακρίνονται στους (1) «μεταβλητούς δι εκλείψεων», (2) «μεταβλητούς βραχείας περιόδου» ή «βραχυπερίοδους μεταβλητούς», και (3) «μεταβλητούς μακράς περιόδου» ή «μακροπερίοδους μεταβλητούς». Ενώ οι μή περιοδικοί μεταβλητοί χωρίζονται στους (1) «ανώμαλους μεταβλητούς», και (2) «καινοϕανείς» (novae) και «υπερκαινοϕανείς» (supernovae). Οι μεταβλητοί δι εκλείψεων μεταβάλλουν τη λαμπρότητά τους επειδή συμμετέχουν (με έναν ακόμη αστέρα που συνήθως λέγεται «συνοδός αστέρας») σε εκλειπτικά ϕαινόμενα. Ολοι οι άλλοι μεταβλητοί οϕείλουν τη μεταβολή της λαμπρότητάς τους στις ϕυσικές συνθήκες που επικρατούν στο εσωτερικό τους δηλαδή τα αίτια της μεταβολής είναι ενδογενή. Στην αστροϕυσική, οι τελευταίοι θεωρούνται πιο ενδιαϕέροντες και συνήθως ονομάζονται «γνήσιοι μεταβλητοί». Εδώ θα εξετάσουμε τους βραχυπερίοδους και μακροπερίοδους μεταβλητούς.
32 2.14 Μεταβλητοί αστέρες 31 Οι βραχυπερίοδοι μεταβλητοί ανήκουν στους ϕασματικούς τύπους από B έως M, αλλά κυρίως στους F και G. Οι μακροπερίοδοι μεταβλητοί έχουν ερυθρό χρώμα και ανήκουν στον ϕασματικό τύπο M. Οι παλλόμενοι αστέρες είναι γνήσιοι μεταβλητοί αστέρες. Ενας τέτοιος αστέρας συστέλλεται και διαστέλλεται διαδοχικά και περιοδικά. Η διαδοχή συστολής διαστολής αναϕέρεται ως «ανάπαλση». Η ανάπαλση συνδέεται με μία έντονη διακύμανση της θερμοκρασίας στο εσωτερικό του αστέρα και αποτελεί το αίτιο μεταβολής της λαμπρότητας. Οι βραχυπερίοδοι μεταβλητοί είναι παλλόμενοι μεταβλητοί αστέρες με περίοδο μικρότερη των 100 ημερών. Από αυτούς, ιδιαίτερο ενδιαϕέρον παρουσιάζουν οι λεγόμενοι «κηϕείδες» (cepheids). Εχουν πάρει το όνομά τους από τον τυπικό εκπρόσωπο αστέρα δ του Κηϕέως (δ Cep). Η περιοδική μεταβολή του ϕαινόμενου μεγέθους του αστέρα αυτού (= «καμπύλη ϕωτός») ϕαίνεται στο Σχήμα 2.5. Η περίοδός του είναι ίση με 5.4 ημέρες. Σχήμα 2.5: Καμπύλη ϕωτός του αστέρα δ του Κηϕέως (δ Cep). Οι κηϕείδες ταξινομούνται στους «κλασικούς κηϕείδες τύπου Ι» και στους «κηϕείδες τύπου Ι Ι». Οι πρώτοι ανήκουν στους «αστέρες του πληθυσμού Ι», δηλαδή βρίσκονται στο γαλαξιακό επίπεδο και κυρίως στις σπείρες του Γαλαξία, οπότε και είναι πλούσιοι σε μέταλλα (= στοιχεία βαρύτερα του ηλίου). Ενώ οι δεύτεροι ανήκουν στους «αστέρες του πληθυσμού Ι Ι», που σημαίνει ότι παρατηρούνται εκτός γαλαξιακού επιπέδου και κυρίως στα σϕαιρωτά αστρικά σμήνη του Γαλαξία τέτοιοι αστέρες είναι πτωχοί σε μέταλλα. Οι κηϕείδες τύπου Ι έχουν κυρίως κίτρινο χρώμα. Εκτός από τον τυπικό τους εκπρόσωπο, γνωστοί είναι ο αστέρας η του Αετού (η Aql) και ο αστέρας ζ των Διδύμων (ζ Gem). Στον Γαλαξία, έχουν παρατηρηθεί 650 τέτοιοι αστέρες με περίοδο 1 50 ημερών, συνήθως δε 5 ημερών. Οι κηϕείδες τύπου Ι Ι έχουν περίοδο 2 75 ημερών. Τυπικός εκπρόσωπος είναι ο αστέρας W Vir. Σε αυτούς ανήκουν οι μεταβλητοί τύπου RR Lyrae, οι οποίοι ονομάζοντια και «μεταβλητοί σμηνών», επειδή παρατηρήθηκαν αρχικά στα σϕαιρωτά αστρικά σμήνη. Οι μεταβλητοί σμηνών έχουν περίοδο ωρών και το κύριο χρώμα τους είναι το κυανό. Ολοι οι παλλόμενοι αστέρες είναι γίγαντες ή υπεργίγαντες.
33 2.14 Μεταβλητοί αστέρες Sqèsh periìdou apìlutou megèjouc, isodônama, periìdou fwteinìthtac Το 1912, η Αμερικανίδα αστρονόμος Henrietta Leavitt διαπίστωσε ότι υπάρχει σχέση μεταξύ της περιόδου και του ϕαινόμενου μεγέθους ενός μεγάλου δείγματος ( 1800) κηϕειδών αστέρων, τους οποίους παρατήρησε στο Μικρό Νέϕος του Μαγγελλάνου. Αυτό είναι ένας μικρός γαλαξίας που βρίσκεται σε απόσταση ly. Λόγω της μεγάλης απόστασής του, οι παρατηρηθέντες κηϕείδες βρίσκονται περίπου στην ίδια απόσταση. Συνεπώς η σχέση περιόδου ϕαινόμενου μεγέθους είναι και σχέση περιόδου απόλυτου μεγέθους, άρα και σχέση περιόδου ϕωτεινότητας. Η Leavitt δεν γνώριζε την απόσταση του γαλαξία αυτού και έτσι δεν μπόρεσε να δώσει τα απόλυτα μεγέθη στη θέση των ϕαινόμενων μεγεθών. Τη μετατροπή, από ϕαινόμενα σε απόλυτα μεγέθη, πέτυχε ο Αμερικανός αστρονόμος Harlow Shapley. Αυτός (1) προσδιόρισε την απόσταση αρκετών κηϕειδών αστέρων του Γαλαξία μας, (2) υπέθεσε ότι σε ίδιες περιόδους αντιστοιχούν ίδια απόλυτα μεγέθη ανεξάρτητα από το σε ποιόν γαλαξία παρατηρήθηκαν οι κηϕείδες, και (3) αναβαθμολόγησε τον άξονα των μεγεθών σε απόλυτα μεγέθη. Με βάση την εργασία του Shapley, εκτιμήθηκαν οι αποστάσεις αρκετών γαλαξιών, μεταξύ των οποίων και ο γαλαξίας της Ανδρομέδας για αυτόν εκτιμήθηκε απόσταση ly. Περί το 1950, ο Walter Baade ανακάλυψε ότι οι κηϕείδες δεν είναι μία ενιαία ομάδα, αλλά διακρίνονται στους κηϕείδες τύπου Ι και στους κηϕείδες τύπου Ι Ι. Αυτοί οι δύο τύποι χαρακτηρίζονται από διαϕορετικές καμπύλες περιόδου απόλυτου μεγέθους, οι οποίες απέχουν μεταξύ τους 1.5 μέγεθος. Το Σχήμα 2.6 παριστάνει γραϕικά τη σχέση περιόδου απόλυτου μεγέθους και για τους δύο τύπους αστέρων. Οι κηϕείδες τύπου Ι Ι της κατηγορίας RR Lyrae έχουν όλοι περίπου το ίδιο απόλυτο μέγεθος, M RR Σχήμα 2.6: Η σχέση περιόδου απολύτου μεγέθους για τους κηϕείδες τύπου Ι (κυανή καμπύλη) και τους κηϕείδες τύπου ΙΙ (ερυθρή καμπύλη).
34 2.14 Μεταβλητοί αστέρες 33 Μετά την ανακάλυψη του Baade, έγινε διόρθωση σε όλες τις μέχρι τότε εκτιμήσεις εξωγαλαξιακών αποστάσεων. Η διαϕορά του 1.5 μεγέθους οδηγεί μέσω της Εξίσωσης 2.10 σε διπλασιασμό των αποστάσεων. Με αυτό το όνομα έμεινε γνωστή στην ιστορία της αστρονομίας η σημαντική διόρθωση των αποστάσεων κατά τη δεκαετία του H jewrða twn anapˆlsewn Το 1914, ο Shapley διατύπωσε τη θεωρία των αναπάλσεων, την οποία και παρουσίασε σε μαθηματική μορϕή ο Άγγλος αστρονόμος Arthur Eddington. Σύμϕωνα με τη θεωρία αυτή, ο αστέρας αναπάλλεται (= συστέλλεται και διαστέλλεται) περιοδικά περί τη θέση θερμικής και υδροστατικής ισορροπίας του. Ενα σημαντικό συμπέρασμα του Eddington ήταν ότι η περίοδος, P, ενός κηϕείδη είναι αντιστρόϕως ανάλογη της τετραγωνικής ρίζας της μέσης πυκνότητας, ρ, του αστέρα, 5.6 P = ρ, (2.53) όπου η περίοδος αντικαθίσταται ή υπολογίζεται σε ώρες και η πυκνότητα αντικαθίσταται ή υπολογίζεται σε g cm 3. Υποθέτοντας ότι οι κηϕείδες έχουν περίπου την ίδια μάζα, μπορούμε να χρησιμοποιήσουμε την Εξίσωση 2.53 για να εξηγήσουμε τη σχέση περιόδου ϕωτεινότητας. Συγκεκριμένα, οι αστέρες μικρότερης ϕωτεινότητας έχουν μικρότερες ακτίνες και, συνεπώς, μεγαλύτερες πυκνότητες. Τότε από την εξίσωση προκύπτει μικρότερη περίοδος. Ενώ οι αστέρες μεγαλύτερης ϕωτεινότητας έχουν μεγαλύτερες ακτίνες και, συνεπώς, μικρότερες πυκνότητες. Οπότε η εξίσωση δίνει μεγαλύτερη περίοδο MakroperÐodoi metablhtoð kai oi jèseic twn pallìmenwn metablht n astèrwn sto diˆgramma H R Οι μακροπερίοδοι μεταβλητοί έχουν περιόδους ημερών. Τυπικό παράδειγμα μακροπερίοδου μεταβλητού είναι ο αστέρας Mira (o Cet). Η περίοδός του κυμαίνεται μεταξύ 320 και 370 ημερών. Ο αστέρας αυτός είναι ένας ερυθρός υπεργίγαντας με μάζα 10M και ακτίνα 300R. Οι μακροπερίοδοι μεταβλητοί είναι υπεργίγαντες ή γίγαντες. Το Σχήμα 2.7 δείχνει τη θέση των μακροπερίοδων μεταβλητών στο άνω δεξιό μέρος του διαγράμματος H R. Στο ίδιο σχήμα, οι κηϕείδες ϕαίνονται μέσα στη λεγόμενη «ζώνη αστάθειας». Αυτή είναι μία περιοχή θερμικής και υδροστατικής αστάθειας για τους γίγαντες και υπεργίγαντες. Οπότε ευνοείται η ανάπαλση ενός αστέρα, ευρισκόμενου εντός της ζώνης, προς αναζήτηση ισορροπίας. Στο κατώτερο σημείο της ζώνης αστάθειας ϕαίνονται και οι μεταβλητοί αστέρες RR Lyrae.
35 2.14 Μεταβλητοί αστέρες 34 Σχήμα 2.7: Η θέση των παλλόμενων μεταβλητών αστέρων στο διάγραμμα H R.
36 Kefˆlaio 3 O GalaxÐac 3.1 Sq ma kai perieqìmeno tou GalaxÐa Οταν είμαστε μακρυά από τα ϕώτα της πόλης και παρατηρούμε τον ουρανό κάποια νύκτα του καλοκαιριού χωρίς ϕεγγάρι και σύννεϕα, τον βλέπουμε να διασχίζεται από μία αμυδρή ϕωτεινή ζώνη. Οι αρχαίοι ονόμαζαν αυτή τη ζώνη Γαλαξία. Ο Δημόκριτος είχε γράψει για αυτόν ότι ο γαλαξίας εστί πολλών τε και μικρών και συνεχών αστέρων, συμϕωτιζομένων αλλήλοις, συναυγασμός δια την πύκνωσιν. Δεν μπορούμε να δούμε ολόκληρο τον Γαλαξία, επειδή είναι ένα γιγαντιαίο σύστημα, το οποίο εμείς επιχειρούμε να παρατηρήσουμε από το εσωτερικό του. Εξάλλου, η απλή έστω παρατήρηση απομακρυσμένων περιοχών του Γαλαξία με τηλεσκόπιο είναι αδύνατη, αϕού τα ϕωτόνια του ορατού ϕάσματος (Σχ. 1.3) απορροϕούνται από την ύλη που γεμίζει τον χώρο μεταξύ των αστέρων του. Μία τυπική περιγραϕή του Γαλαξία έχει ως εξής. Η «κεντρική περιοχή» (galactic bulge) έχει σϕαιροειδές σχήμα μικρής πλάτυνσης (η σϕαίρα περιγράϕεται πλήρως από την ακτίνα της το σϕαιροειδές περιγράϕεται από τον μεγάλο και μικρό ημιάξονά του, a και b, με πλάτυνση a b a και μέση ακτίνα a+b 2 ). Η μέση ακτίνα της κεντρικής περιοχής είναι 6 kpc ( 20 kly). Ο «γαλαξιακός πυρήνας» (galactic nucleus) βρίσκεται στο κέντρο της περιοχής αυτής. Εδώ οι αστέρες έχουν εξαιρετικά μεγάλη πυκνότητα, εκατομμύρια ϕορές μεγαλύτερη από την πυκνότητα των αστέρων στην περιοχή του Ηλιου. Οι παρατηρήσεις οδηγούν σε ενδείξεις για την ύπαρξη μίας γιγάντειας μελανής οπής στον γαλαξιακό πυρήνα με μάζα M. Ο «γαλαξιακός δίσκος» (galactic disk) έχει διάμετρο 40 kpc ( 120 kly) και μέσο πάχος 2 kpc. Στη βιβλιογραϕία, ο γαλαξιακός δίσκος λέγεται συχνά και «γαλαξιακό επίπεδο» (galactic plane). Εδώ βρίσκεται συγκεντρωμένη η περισσότερη ύλη του Γαλαξία. Η παρατήρηση και μελέτη του γαλαξιακού δίσκου έγινε με τη βοήθεια της ραδιοαστρονομίας. Οι σχετικές έρευνες έδειξαν ότι ο Γαλαξίας έχει σπειροειδή μορϕή (= «σπειροειδής γαλαξίας»), με τις σπείρες του να βρίσκονται επάνω στον γαλαξιακό δίσκο. Ο Ηλιος βρίσκεται σε μία από τις σπείρες, απέχει από το κέντρο 10 kpc ( 30 kly), και περιστρέϕεται γύρω από αυτό με περίοδο y. Η περίοδος αυτή λέγεται «κοσμικό έτος». Η ταχύτητα του Ηλιου στην κυκλική τροχιά του είναι 250 km s 1. Η «άλως» (halo) του Γαλαξία εκτείνεται στον χώρο μίας σϕαίρας με ακτίνα kpc ( kly). Είναι το γηραιότερο τμήμα του Γαλαξία. Περιέχει 35
37 3.2 Σϕαιρωτά αστρικά σμήνη 36 κυρίως τα σϕαιρωτά αστρικά σμήνη, τα οποία είναι σϕαιρικές συγκεντρώσεις αστέρων. Υπάρχουν ενδείξεις ότι η άλως μπορεί να περιέχει και «σκοτεινή ύλη» (dark matter), η οποία, σύμϕωνα με τις νέες θεωρίες της ϕυσικής, δεν αλληλεπιδρά με την ηλεκτρομαγνητική ακτινοβολία όπως η συνήθης ύλη. Δεν μπορούμε λοιπόν να την δούμε, μπορούμε όμως να την παρατηρήσουμε μέσω της βαρυτικής της αλληλεπίδρασης με τη συνήθη ύλη. Ο Γαλαξίας περιέχει αστέρες, μεσοαστρική ύλη και μεσοαστρική ακτινοβολία. Συγκεκριμένα, υπάρχουν αστέρες, οι οποίοι συνήθως συγκροτούν συγκεντρώσεις διαϕορετικού πλήθους. Οι συγκεντρώσεις αυτές ονομάζονται «αστρικά σμήνη» (stellar clusters). Αυτά διακρίνονται σε «σϕαιρωτά αστρικά σμήνη» (globular stellar clusters) και σε «ανοικτά αστρικά σμήνη» (open stellar clusters). 3.2 Sfairwtˆ astrikˆ sm nh Τα σϕαιρωτά σμήνη είναι σϕαιρικές συγκεντρώσεις αστέρων. Ενα σϕαιρωτό σμήνος δημιουργείται από τον μηχανισμό αστάθειας βαρύτητας του Jeans. Συγκεκριμένα, η βαρύτητα μπορεί να ευνοήσει μία μικρή τοπική διακύμανση της πυκνότητας μίας υλικής κατανομής και έτσι να οδηγήσει στη δημιουργία ενός μορϕώματος με δικό του πεδίο βαρύτητας το σϕαιρωτό σμήνος είναι ένα τέτοιο μόρϕωμα. Τα σϕαιρωτά σμήνη έχουν διάμετρο pc. Η πυκνότητα των αστέρων κοντά στο κέντρο ενός σϕαιρωτού σμήνους είναι αστέρες pc 3. Εχουν παρατηρηθεί 150 σϕαιρωτά σμήνη στην άλω του Γαλαξία, ενώ ο συνολικός αριθμός τους (στον Γαλαξία) υπολογίζεται σε 200. Από τη μελέτη των σϕαιρωτών σμηνών με τη βοήθεια του διαγράμματος H R, προκύπτει ότι αυτά έχουν ηλικία y είναι δηλαδή τα πιο ηλικιωμένα μέλη του Γαλαξία. Ενας υποθετικός πολιτισμός σε έναν πλανήτη ενός από τους αστέρες τέτοιου σμήνους θα αντίκρυζε κάθημερινά ένα ϕανταστικό θέαμα. Στον ουρανό θα έλαμπαν αστέρες, από τους οποίους πολλοί θα είχαν πολύ μεγάλη λαμπρότητα. Το ϕως του νυκτερινού ουρανού θα ήταν πολύ πιο έντονο από το ϕως της αυγής στη Γη μας. 3.3 Anoiktˆ astrikˆ sm nh Τα ανοικτά σμήνη έχουν αστέρες σε σχετικά αραιή διάταξη. Σε αντίθεση με τα σϕαιρωτά σμήνη που κατοικούν στην άλω του Γαλαξία, τα ανοικτά σμήνη βρίσκονται στον γαλαξιακό δίσκο. Εχουν διάμετρο 2 20 pc. Η πυκνότητα των αστέρων κοντά στο κέντρο ενός ανοικτού σμήνους είναι 5 αστέρες pc 3. Εχουν παρατηρηθεί 10 3 ανοικτά σμήνη, ο δε συνολικός αριθμός τους (στον Γαλαξία) υπολογίζεται σε Τα νεότερα ανοικτά σμήνη, όπως το ζεύγος h και ξ του Περσέα, έχουν ηλικία y. Οι Πλειάδες του Ταύρου έχουν ηλικία y, ενώ οι Υάδες του Ταύρου y. Υπάρχει μία σαϕής διάκριση μεταξύ των νεότερων και των παλαιότερων ανοικτών σμηνών. Συγκεκριμένα, τα νεότερα ϕαίνονται πυκνότερα, ενώ τα παλαιότερα είναι αραιότερα και δείχνουν να οδεύουν σε διάλυση.
38 3.4 Αστρικοί πληθυσμοί AstrikoÐ plhjusmoð Ανάλογα με τη χημική τους σύσταση και την ηλικία τους, οι αστέρες του Γαλαξία ανήκουν στον «αστρικό πληθυσμό Ι» ή στον «αστρικό πληθυσμό Ι Ι». Συγκεκριμένα, στον πληθυσμό Ι περιέχονται αστέρες πολύ νέοι σε ηλικία, των οποίων η χημική σύσταση είναι πλούσια σε μέταλλα (στην αστροϕυσική, ως μέταλλα αναϕέρονται όλα τα στοιχεία τα βαρύτερα του ηλίου). Στον πληθυσμό Ι Ι ανήκουν κυρίως οι αστέρες των σϕαιρωτών αστρικών σμηνών. Οι αστέρες αυτοί είναι μεγάλης ηλικίας ( y) η περιεκτικότητά τους σε μέταλλα είναι μόλις 1 10 εκείνης του πληθυσμού Ι. 3.5 Mesoastrik Ôlh Η ύλη που υπάρχει μεταξύ των αστέρων του Γαλαξία ονομάζεται «μεσοαστρική ύλη»(interstellar medium). Η ύλη αυτή έχει πρωτογενή και δευτερογενή προέλευση, δηλαδή μερικώς είναι το αρχέγονο υλικό που δημιούργησε τον γαλαξία και μερικώς είναι το υλικό που εκτινάσσεται στον μεσοαστρικό χώρο όταν καταστρέϕονται με εκρηκτικό τρόπο προϋπάρχοντες αστέρες (π.χ., οι υπερκαινοϕανείς αστέρες). Η μεσοαστρική ύλη αποτελείται κυρίως από ουδέτερο υδρογόνο (Η Ι), από ιονισμένο υδρογόνο (Η Ι Ι), από άλλα βαρύτερα στοιχεία και μόρια σε μικρότερη αναλογία. Τα συστατικά της μεσοαστρικής ύλης έχουν τη μορϕή αερίου, οπότε κάνουμε λόγο για το «μεσοαστρικό αέριο», και τη μορϕή σκόνης, οπότε κάνουμε λόγο για τη «μεσοαστρική σκόνη». Η τυπική πυκνότητα της μεσοαστρικής ύλης είναι 0.8 άτομα cm 3 ή g cm 3. Η τυπική χημική σύστασή της είναι 70 80% υδρογόνο, 96 98% υδρογόνο και ήλιο μαζί, και το υπόλοιπο ποσοστό αποτελείται από βαρύτερα στοιχεία. Το μεσοαστρικό αέριο απότελείται κατά 95% από ουδέτερα άτομα και μόρια, και κατά 5% από ιονισμένη ύλη. 3.6 Mesoastrikˆ nefel mata Ορισμένες μεσοαστρικές περιοχές έχουν μεγαλύτερη πυκνότητα μεσοαστρικής ύλης, δηλαδή άτομα cm 3. Οι περιοχές αυτές ονομάζονται «μεσοαστρικά νε- ϕελώματα» (interstellar nebulae). Τα «ϕωτεινά νεϕελώματα» (bright nebulae) αποτελούνται κυρίως από ιονισμένο υδρογόνο (Η Ι Ι, «περιοχές Η Ι Ι»), το οποίο διεγείρεται από την ακτινοβολία των αστέρων που περιέχονται σε αυτά (ϕασματικών τύπων από O5 έως B1). Στην περίπτωση αυτή, κάνουμε λόγο για «νεϕελώματα εκπομπής» (emission nebulae). Οι διαστάσεις των νεϕελωμάτων αυτών είναι pc. Γνωστό είναι το νεϕέλωμα εκπομπής του Ωρίωνα. Οταν τα ϕωτεινά νεϕελώματα έχουν αρκετή μεσοαστρική σκόνη, τότε ανακλούν το ϕως των αστέρων που περιέχονται σε αυτά (ϕασματικών τύπων B2 έως A0). Συνεπώς το ϕως τους δεν εκπέμπεται από αυτά τα ίδια, αλλά είναι ανακλώμενο ϕως από τους αστέρες τους οποίους περιβάλλουν. Για αυτό τον λόγο, λέγονται «νεϕελώματα ανάκλασης» (reflection nebulae). Τα «σκοτεινά νεϕελώματα» (dark nebulae) έχουν την ίδια σύσταση με τα προηγούμενα, αλλά δεν περιβάλλουν αστέρες, ούτε βρίσκονται κοντά σε αστέρες. Το απότέλεσμα είναι να μην ϕωτίζονται από εκπομπή ή ανάκλαση και να παραμένουν σκοτεινά. Η διάμετρός τους είναι μερικές εκατοντάδες παρσέκ.
39 3.7 Μεσοαστρική ακτινοβολία Mesoastrik aktinobolða Η μεσοαστρική ακτινοβολία αποτελείται από την ακτινοβολία των 21 cm του ουδέτερου υδρογόνου, «συνεχή ραδιοεκπομπή», «ακτινοβολία X και γ», και «κοσμική ακτινοβολία». Η ακτινοβολία των 21 cm εκπέμπεται από τα «νέϕη ουδέτερου υδρογόνου» (Η Ι, «περιοχές Η Ι»). Αυτή οϕείλεται στην υπέρλεπτη υϕή της θεμελιώδους στάθμης του ατόμου του υδρογόνου. Συγκεκριμένα, το spin του περιϕερειακού ηλεκτρόνιου είναι δυνατό να μεταπέσει από θέση παράλληλη, ως προς το spin του πρωτόνιου στον πυρήνα, σε θέση αντιπαράλληλη. Οι δύο αυτές στάθμες έχουν μικρή ενεργειακή διαϕορά και η συχνότητα της εκπεμπόμενης ηλεκτρομαγνητικής ακτινοβολίας (Εξ. 1.25, 1.27) είναι ν HI = MHz που αντιστοιχεί σε μήκος κύματος λ HI 21 cm. Σύμϕωνα με την κβαντομηχανική, η πιθανότητα για την πραγματοποίηση μίας μετάπτωσης στο spin του ηλεκτρόνιου είναι εξαιρετικά μικρή. Ομως το ουδέτερο υδρογόνο είναι άϕθονο στον Γαλαξία, οπότε η χαρακτηριστική γραμμή των 21 cm ανιχνεύεται έντονα. Στη βιβλιογραϕία (κυρίως την εκλαϊκευμένη), η ηλεκτρομαγνητική ακτινοβολία των 21 cm του ουδέτερου υδρογόνου λέγεται συχνά μουσική του Γαλαξία ή γαλαξιακή μουσική. 3.8 H mˆza tou GalaxÐa Upologismìc thc mˆzac apì thn kampôlh peristrof c tou GalaxÐa Ενας τρόπος υπολογισμού της μάζας του Γαλαξία προκύπτει από την παρατηρούμενη «καμπύλη περιστροϕής», δηλαδή από τον τρόπο με τον οποίο μεταβάλλεται η τροχιακή ταχύτητα, υ, με την απόσταση από το γαλαξιακό κέντρο, r. Εξισώνοντας το μέτρο της κεντρομόλου δύναμης, m(r) υ(r) 2 /r όπου m(r) η μάζα στο r, με το μέτρο της βαρυτικής έλξης, G M(r) m(r)/r 2 όπου M(r) η μάζα του Γαλαξία μέχρι την απόσταση r, και λύνοντας ως προς τη μάζα M(r), βρίσκουμε M(r) = r υ(r)2 G. (3.1) Στο Σχήμα 3.1 δίνεται η παρατηρούμενη καμπύλη περιστροϕής του Γαλαξία μας. Από το διάγραμμα αυτό διαπιστώνουμε ότι οι τροχιακές ταχύτητες δεν έχουν Κεπλεριανή συμπεριϕορά με την έννοια ότι δεν ισχύει για αυτές ο τρίτος νόμος του Kepler. Για το Ηλιακό Σύστημα, ο νόμος αυτός έχει την ακόλουθη διατύπωση: «ο λόγος του τετραγώνου της περιόδου ενός πλανήτη προς τον κύβο του μεγάλου ημιάξονα της ελλειπτικής τροχιάς του είναι σταθερός». Συγκεκριμένα, παριστάνοντας με P την περίοδο ενός πλανήτη και θεωρώντας για αυτόν κυκλική τροχιά ακτίνας a (η περίπτωση ελλειπτικής τροχιάς με μεγάλο ημιάξονα a δεν διαϕέρει ριζικα), παίρνουμε τη σχέση P = 2 π a υ. (3.2) Με χρήση αυτής, απαλείϕουμε το υ από την ισότητα μεταξύ κεντρομόλου δύναμης και βαρυτικής έλξης, αναδιατάσσουμε τους όρους, και βρίσκουμε P 2 = 4 π2 G M a 3. (3.3)
40 3.8 Η μάζα του Γαλαξία 39 Σχήμα 3.1: Η ταχύτητα περιστροϕής του Γαλαξία ως συνάρτηση της απόστασης από το γαλαξιακό κέντρο. 4π Ο συντελεστής 2 GM είναι μία σταθερά για το Ηλιακό Σύστημα, οπότε το τετράγωνο της περιόδου προκύπτει ανάλογο του κύβου της ακτίνας. Εναλλακτικά, μπορούμε να απαλείψουμε από την Εξίσωση 3.3 το P με χρήση της Εξίσωσης 3.2, και να πάρουμε τη σχέση υ = 1 G M a, (3.4) που εκϕράζει την Κεπλεριανή συμπεριϕορά της τροχιακής ταχύτητας, δηλαδή ότι αυτή είναι αντιστρόϕως ανάλογη προς την τετραγωνική ρίζα της ακτίνας. Η Κεπλεριανή συμπεριϕορά χαρακτηρίζει κάθε ϕυσικό σύστημα του οποίου η μάζα βρίσκεται σχεδόν όλη στο κεντρικό σώμα (η μάζα του Ηλιακού Συστήματος είναι σχεδόν όλη συγκεντρωμένη στον Ηλιο). Από το Σχήμα 3.1 ϕαίνεται ότι η τροχιακή ταχύτητα δεν μεταβάλλεται όπως ορίζει η Εξίσωση 3.4, συνεπώς η μάζα του Γαλαξία δεν είναι συγκεντρωμένη μόνον στην κεντρική περιοχή του. Αυτό σημαίνει ότι υπάρχει άϕθονη ύλη στην άλω του Γαλαξία, αλλά και πέραν του ορατού άκρου της, που όμως δεν έχει καταστεί δυνατό να ανιχνευθεί με οπτικές παρατηρήσεις. Οπως αναϕέρεται και στην 3.1, εικάζεται ότι η άλως μπορεί να περιέχει σκοτεινή ύλη που δεν αλληλεπιδρά με την ηλεκτρομαγνητική ακτινοβολία μπορεί να παρατηρηθεί μόνο μέσω της βαρυτικής αλληλεπίδρασής της με τη συνήθη ύλη. Θέτοντας στην Εξίσωση 3.1 r 70 kpc και υ 250 km s 1, παίρνουμε ως εκτίμηση για τη μάζα του Γαλαξία μας M Γ M. Η εκτίμηση αυτή είναι 5 10 ϕορές μεγαλύτερη από τις τιμές που αναϕέρονται σε παλαιότερα βιβλία Κοσμολογίας Upologismìc thc mˆzac apì to Je rhma Virial Το Θεώρημα Virial αναϕέρεται σε συστήματα των οποίων η μορϕή παραμένει κατά μέσον όρο σταθερή δεν αλλάζει με τον χρόνο. Για τέτοια συστήματα, το άθροισμα της βαρυτικής δυναμικής ενέργειας, W, και του διπλάσιου της κινητικής ενέργειας, T, είναι ίσο με το μηδέν, W + 2 T = 0. (3.5)
Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών
 Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών Το φως που έρχεται από τα άστρα είναι σύνθετο και καλύπτει ολόκληρο το εύρος της ηλεκτρομαγνητικής ακτινοβολίας.
Το Φως της Αστροφυσικής Αν. καθηγητής Στράτος Θεοδοσίου Πρόεδρος της Ένωσης Ελλήνων Φυσικών Το φως που έρχεται από τα άστρα είναι σύνθετο και καλύπτει ολόκληρο το εύρος της ηλεκτρομαγνητικής ακτινοβολίας.
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Η γέννηση της Αστροφυσικής Οι αστρονόμοι μελετούν τα ουράνια σώματα βασισμένοι στο φως, που λαμβάνουν από αυτά. Στα πρώτα χρόνια των παρατηρήσεων,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Η γέννηση της Αστροφυσικής Οι αστρονόμοι μελετούν τα ουράνια σώματα βασισμένοι στο φως, που λαμβάνουν από αυτά. Στα πρώτα χρόνια των παρατηρήσεων,
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙΔΑΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΟΦΡΟΝΤΙΣΤΗΡΙΑΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 3 ΙΑΝΟΥΑΡΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α. Στις
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΟΦΡΟΝΤΙΣΤΗΡΙΑΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 3 ΙΑΝΟΥΑΡΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Α. Στις
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011
 Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011 Patra, 11 Febrouariou 2011 1 Jèma 1 1.1 DiatÔpwsh Στην αριθμητική διαπραγμάτευση ενός κοσμολογικού μοντέλου εμπλέκονται οι ρίζες ενός «χαρακτηριστικού
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2011 Patra, 11 Febrouariou 2011 1 Jèma 1 1.1 DiatÔpwsh Στην αριθμητική διαπραγμάτευση ενός κοσμολογικού μοντέλου εμπλέκονται οι ρίζες ενός «χαρακτηριστικού
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 η - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 14/09/2014 ΘΕΜΑ Α Α1. Κατά την ανάλυση λευκού φωτός από γυάλινο πρίσμα, η γωνία εκτροπής του κίτρινου χρώματος είναι:
προς τα θετικά του x άξονα. Ως κύμα η ηλεκτρομαγνητική ακτινοβολία (άρα και το φως) ικανοποιούν τη βασική εξίσωση των κυμάτων, δηλαδή: c = λf (1)
 Φως 1 1 Φως 11 Η φύση του φωτός Το φως είναι το μέρος της ηλεκτρομαγνητικής ακτινοβολίας που διεγείρει τα κωνία και τα ραβδία του αμφιβληστροειδή χιτώνα του ματιού μας Αυτό έχει μήκος κύματος από λ 400
Φως 1 1 Φως 11 Η φύση του φωτός Το φως είναι το μέρος της ηλεκτρομαγνητικής ακτινοβολίας που διεγείρει τα κωνία και τα ραβδία του αμφιβληστροειδή χιτώνα του ματιού μας Αυτό έχει μήκος κύματος από λ 400
είναι τα μήκη κύματος του φωτός αυτού στα δύο υλικά αντίστοιχα, τότε: γ. 1 Β) Να δικαιολογήσετε την επιλογή σας.
 Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
Β.1 Μονοχρωματικό φως, που διαδίδεται στον αέρα, εισέρχεται ταυτόχρονα σε δύο οπτικά υλικά του ίδιου πάχους d κάθετα στην επιφάνειά τους, όπως φαίνεται στο σχήμα. Οι χρόνοι διάδοσης του φωτός στα δύο υλικά
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΕΚΦΩΝΗΣΕΙΣ. Στις παρακάτω ερωτήσεις 1-4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ Στις παρακάτω ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ο λαµπτήρας φθορισµού:
Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ ΦΥΣΙΚΗ Στις παρακάτω ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ο λαµπτήρας φθορισµού:
Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών
 Ο11 Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών 1. Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί α) στην μελέτη του φαινομένου της εξασθένησης του φωτός καθώς αυτό διέρχεται
Ο11 Απορρόφηση του φωτός Προσδιορισμός του συντελεστή απορρόφησης διαφανών υλικών 1. Σκοπός Η εργαστηριακή αυτή άσκηση αποσκοπεί α) στην μελέτη του φαινομένου της εξασθένησης του φωτός καθώς αυτό διέρχεται
Το φως διαδίδεται σε όλα τα οπτικά υλικά μέσα με ταχύτητα περίπου 3x10 8 m/s.
 Κεφάλαιο 1 Το Φως Το φως διαδίδεται σε όλα τα οπτικά υλικά μέσα με ταχύτητα περίπου 3x10 8 m/s. Το φως διαδίδεται στο κενό με ταχύτητα περίπου 3x10 8 m/s. 3 Η ταχύτητα του φωτός μικραίνει, όταν το φως
Κεφάλαιο 1 Το Φως Το φως διαδίδεται σε όλα τα οπτικά υλικά μέσα με ταχύτητα περίπου 3x10 8 m/s. Το φως διαδίδεται στο κενό με ταχύτητα περίπου 3x10 8 m/s. 3 Η ταχύτητα του φωτός μικραίνει, όταν το φως
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009
 Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009 1. Μία περιοχή στο μεσοαστρικό χώρο με ερυθρωπή απόχρωση είναι a. Ο ψυχρός πυρήνας ενός μοριακού νέφους b. Μία περιοχή θερμού ιονισμένου αερίου c. Μία περιοχή
Αστροφυσική ΙΙ Tεστ II- 16 Ιανουαρίου 2009 1. Μία περιοχή στο μεσοαστρικό χώρο με ερυθρωπή απόχρωση είναι a. Ο ψυχρός πυρήνας ενός μοριακού νέφους b. Μία περιοχή θερμού ιονισμένου αερίου c. Μία περιοχή
ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ
 ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ Πολυχρόνης Καραγκιοζίδης Mcs χημικός www.polkarag.gr Μετά τη δημιουργία του Σύμπαντος 380.000 έτη 6000 ο C Τα ηλεκτρόνια μπορούν να συνδεθούν με τα πρωτόνια ή τους άλλους
ΓΕΝΝΗΣΗ ΕΞΕΛΙΞΗ ΚΑΙ ΘΑΝΑΤΟΣ ΑΣΤΕΡΩΝ Πολυχρόνης Καραγκιοζίδης Mcs χημικός www.polkarag.gr Μετά τη δημιουργία του Σύμπαντος 380.000 έτη 6000 ο C Τα ηλεκτρόνια μπορούν να συνδεθούν με τα πρωτόνια ή τους άλλους
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών. Κοσμάς Γαζέας
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Το Ηλιακό Σύστημα Το Ηλιακό Σύστημα αποτελείται κυρίως από τον Ήλιο και τους πλανήτες που περιφέρονται γύρω από αυτόν. Πολλά και διάφορα ουράνια
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Κοσμάς Γαζέας Το Ηλιακό Σύστημα Το Ηλιακό Σύστημα αποτελείται κυρίως από τον Ήλιο και τους πλανήτες που περιφέρονται γύρω από αυτόν. Πολλά και διάφορα ουράνια
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β )
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 13/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΤΡΕΙΣ (13) ΟΔΗΓΙΕΣ ΑΥΤΟΔΙΟΡΘΩΣΗΣ Στις ερωτήσεις Α1
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 13/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΤΡΕΙΣ (13) ΟΔΗΓΙΕΣ ΑΥΤΟΔΙΟΡΘΩΣΗΣ Στις ερωτήσεις Α1
ΘΕΜΑ Β Β.1 Α) Μονάδες 4 Μονάδες 8 Β.2 Α) Μονάδες 4 Μονάδες 9
 Β.1 O δείκτης διάθλασης διαφανούς υλικού αποκλείεται να έχει τιμή: α. 0,8 β. 1, γ. 1,4 Β. Το ηλεκτρόνιο στο άτομο του υδρογόνου, έχει κινητική ενέργεια Κ, ηλεκτρική δυναμική ενέργεια U και ολική ενέργεια
Β.1 O δείκτης διάθλασης διαφανούς υλικού αποκλείεται να έχει τιμή: α. 0,8 β. 1, γ. 1,4 Β. Το ηλεκτρόνιο στο άτομο του υδρογόνου, έχει κινητική ενέργεια Κ, ηλεκτρική δυναμική ενέργεια U και ολική ενέργεια
ΟΡΟΣΗΜΟ ΘΕΜΑ Δ. Δίνονται: η ταχύτητα του φωτός στο κενό c 0 = 3 10, η σταθερά του Planck J s και για το φορτίο του ηλεκτρονίου 1,6 10 C.
 Σε μια διάταξη παραγωγής ακτίνων X, η ηλεκτρική τάση που εφαρμόζεται μεταξύ της ανόδου και της καθόδου είναι V = 25 kv. Τα ηλεκτρόνια ξεκινούν από την κάθοδο με μηδενική ταχύτητα, επιταχύνονται και προσπίπτουν
Σε μια διάταξη παραγωγής ακτίνων X, η ηλεκτρική τάση που εφαρμόζεται μεταξύ της ανόδου και της καθόδου είναι V = 25 kv. Τα ηλεκτρόνια ξεκινούν από την κάθοδο με μηδενική ταχύτητα, επιταχύνονται και προσπίπτουν
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
(Β' Τάξη Εσπερινού) Έργο Ενέργεια
 Φυσική Α' Γενικού Λυκείου (Α' Τάξη Εσπερινού) Ευθύγραμμες Κινήσεις: Ομαλή Ομαλά μεταβαλλόμενη Μεγέθη κινήσεων Χρονική στιγμή χρονική διάρκεια Θέση Μετατόπιση Ταχύτητα (μέση στιγμιαία) Επιτάχυνση Εξισώσεις
Φυσική Α' Γενικού Λυκείου (Α' Τάξη Εσπερινού) Ευθύγραμμες Κινήσεις: Ομαλή Ομαλά μεταβαλλόμενη Μεγέθη κινήσεων Χρονική στιγμή χρονική διάρκεια Θέση Μετατόπιση Ταχύτητα (μέση στιγμιαία) Επιτάχυνση Εξισώσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 204 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 204 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ Θέµα 1 ο 1. Σύµφωνα µε το πρότυπο του Bohr για το άτοµο του υδρογόνου: α) το ηλεκτρόνιο εκπέµπει
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ Θέµα 1 ο 1. Σύµφωνα µε το πρότυπο του Bohr για το άτοµο του υδρογόνου: α) το ηλεκτρόνιο εκπέµπει
ΑΣΚΗΣΗ 5. Ερωτήσεις προετοιμασίας (Να απαντηθούν στην εργαστηριακή αναφορά)
 ΑΣΚΗΣΗ 5 Ερωτήσεις προετοιμασίας (Να απαντηθούν στην εργαστηριακή αναφορά) 1. Χαρακτηρίστε τα παρακάτω φάσματα α) συνεχές β) γραμμικό γ) μετατοπισμένο λόγω Doppler δ) απορρόφησης ε) μη αναλυμένο δ) άλλο
ΑΣΚΗΣΗ 5 Ερωτήσεις προετοιμασίας (Να απαντηθούν στην εργαστηριακή αναφορά) 1. Χαρακτηρίστε τα παρακάτω φάσματα α) συνεχές β) γραμμικό γ) μετατοπισμένο λόγω Doppler δ) απορρόφησης ε) μη αναλυμένο δ) άλλο
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 20 ΜΑΪΟΥ 2015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Al + He X + n, ο πυρήνας Χ είναι:
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 10 IOYNIOY 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 10 IOYNIOY 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 15/9/2013 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΑΣMAΤΙΚΗ ΤΑΞΙΝΟΜΗΣΗ ΑΣΤΕΡΩΝ
 ΦΑΣMAΤΙΚΗ ΤΑΞΙΝΟΜΗΣΗ ΑΣΤΕΡΩΝ Εισαγωγή στην κβαντομηχανική και στην ατομική Φυσική ΦΩΣ = Ηλεκτρομαγνητικό κύμα με σωματιδιακές ιδιότητες (δυική φύση) Τα «σωματίδια» του φωτός ονομάζονται ΦΩΤΟΝΙΑ και έχουν
ΦΑΣMAΤΙΚΗ ΤΑΞΙΝΟΜΗΣΗ ΑΣΤΕΡΩΝ Εισαγωγή στην κβαντομηχανική και στην ατομική Φυσική ΦΩΣ = Ηλεκτρομαγνητικό κύμα με σωματιδιακές ιδιότητες (δυική φύση) Τα «σωματίδια» του φωτός ονομάζονται ΦΩΤΟΝΙΑ και έχουν
Πληροφορίες για τον Ήλιο:
 Πληροφορίες για τον Ήλιο: 1) Ηλιακή σταθερά: F ʘ =1.37 kw m -2 =1.37 10 6 erg sec -1 cm -2 2) Απόσταση Γης Ήλιου: 1AU (~150 10 6 km) 3) L ʘ = 3.839 10 26 W = 3.839 10 33 erg sec -1 4) Διαστάσεις: Η διάμετρος
Πληροφορίες για τον Ήλιο: 1) Ηλιακή σταθερά: F ʘ =1.37 kw m -2 =1.37 10 6 erg sec -1 cm -2 2) Απόσταση Γης Ήλιου: 1AU (~150 10 6 km) 3) L ʘ = 3.839 10 26 W = 3.839 10 33 erg sec -1 4) Διαστάσεις: Η διάμετρος
Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ
 Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ ΑΣΚΗΣΗ 1 Άτομα αερίου υδρογόνου που βρίσκονται στη θεμελιώδη κατάσταση (n = 1), διεγείρονται με κρούση από δέσμη ηλεκτρονίων που έχουν επιταχυνθεί από διαφορά δυναμικού
Η ΕΝΕΡΓΕΙΑ ΤΟΥ ΑΤΟΜΟΥ ΤΟΥ ΥΔΡΟΓΟΝΟΥ ΑΣΚΗΣΗ 1 Άτομα αερίου υδρογόνου που βρίσκονται στη θεμελιώδη κατάσταση (n = 1), διεγείρονται με κρούση από δέσμη ηλεκτρονίων που έχουν επιταχυνθεί από διαφορά δυναμικού
ΕΚΦΩΝΗΣΕΙΣ. Στις παρακάτω ερωτήσεις 1-4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 008 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις -, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση..
Επαναληπτικά Θέµατα ΟΕΦΕ 008 Γ' ΛΥΚΕΙΟΥ ΕΠΙΛΟΓΗΣ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω ερωτήσεις -, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση..
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ
 ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
Αστρονομία. Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων. Νικόλαος Στεργιούλας Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
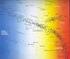 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστρονομία Ενότητα # 4: Χαρακτηριστικά Μεγέθη Αστέρων Νικόλαος Στεργιούλας Τμήμα Φυσικής Αριστοτέιο Πανεπιστήμιο Θεσσαλονίκης Άδειες Χρήσης
ιστοσελίδα μαθήματος
 ιστοσελίδα μαθήματος http://ecourses.chemeng.ntua.gr/courses/inorganic_chemistry/ Είσοδος ως χρήστης δικτύου ΕΜΠ Ανάρτηση υλικού μαθημάτων Μάζα ατόμου= 10-24 kg Πυκνότητα πυρήνα = 10 6 tn/cm 3 Μάζα πυρήνα:
ιστοσελίδα μαθήματος http://ecourses.chemeng.ntua.gr/courses/inorganic_chemistry/ Είσοδος ως χρήστης δικτύου ΕΜΠ Ανάρτηση υλικού μαθημάτων Μάζα ατόμου= 10-24 kg Πυκνότητα πυρήνα = 10 6 tn/cm 3 Μάζα πυρήνα:
Ακτίνες επιτρεπόμενων τροχιών (2.6)
 Αντικαθιστώντας το r με r n, έχουμε: Ακτίνες επιτρεπόμενων τροχιών (2.6) Αντικαθιστώντας n=1, βρίσκουμε την τροχιά με τη μικρότερη ακτίνα n: Αντικαθιστώντας την τελευταία εξίσωση στη 2.6, παίρνουμε: Αν
Αντικαθιστώντας το r με r n, έχουμε: Ακτίνες επιτρεπόμενων τροχιών (2.6) Αντικαθιστώντας n=1, βρίσκουμε την τροχιά με τη μικρότερη ακτίνα n: Αντικαθιστώντας την τελευταία εξίσωση στη 2.6, παίρνουμε: Αν
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 1 Η υπέρυθρη ακτινοβολία α συμμετέχει στη μετατροπή του οξυγόνου της ατμόσφαιρας σε όζον β προκαλεί φωσφορισμό γ διέρχεται μέσα από την ομίχλη και τα σύννεφα δ έχει μικρότερο μήκος κύματος από την υπεριώδη
1 Η υπέρυθρη ακτινοβολία α συμμετέχει στη μετατροπή του οξυγόνου της ατμόσφαιρας σε όζον β προκαλεί φωσφορισμό γ διέρχεται μέσα από την ομίχλη και τα σύννεφα δ έχει μικρότερο μήκος κύματος από την υπεριώδη
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 5 ΧΡΟΝΙΑ ΕΜΠΕΙΡΙΑ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ερωτήσεις Α-Α να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή φράση, η οποία
5 ΧΡΟΝΙΑ ΕΜΠΕΙΡΙΑ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ερωτήσεις Α-Α να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή φράση, η οποία
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 6 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1- να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΛΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΛΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΛΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
Α1. Πράσινο και κίτρινο φως προσπίπτουν ταυτόχρονα και µε την ίδια γωνία πρόσπτωσης σε γυάλινο πρίσµα. Ποιά από τις ακόλουθες προτάσεις είναι σωστή:
 54 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΣΑΒΒΑΪΔΗ-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Φιλολάου & Εκφαντίδου 26 : Τηλ.: 2107601470 ΔΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ 2014 ΘΕΜΑ Α Α1. Πράσινο και κίτρινο φως
54 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΣΑΒΒΑΪΔΗ-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Φιλολάου & Εκφαντίδου 26 : Τηλ.: 2107601470 ΔΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ 2014 ΘΕΜΑ Α Α1. Πράσινο και κίτρινο φως
ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ
 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ Απεικόνιση ηλεκτρονίων ατόμων σιδήρου ως κύματα, διατεταγμένων κυκλικά σε χάλκινη επιφάνεια, με την τεχνική μικροσκοπικής σάρωσης σήραγγας. Δημήτρης
ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ ΚΑΙ ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ Απεικόνιση ηλεκτρονίων ατόμων σιδήρου ως κύματα, διατεταγμένων κυκλικά σε χάλκινη επιφάνεια, με την τεχνική μικροσκοπικής σάρωσης σήραγγας. Δημήτρης
Γραμμικά φάσματα εκπομπής
 Γραμμικά φάσματα εκπομπής Η Ηe Li Na Ca Sr Cd Οι γραμμές αντιστοιχούν σε ορατό φως που εκπέμπεται από διάφορα άτομα. Ba Hg Tl 400 500 600 700 nm Ποιο φάσμα χαρακτηρίζεται ως γραμμικό; Σχισμή Πρίσμα Φωτεινή
Γραμμικά φάσματα εκπομπής Η Ηe Li Na Ca Sr Cd Οι γραμμές αντιστοιχούν σε ορατό φως που εκπέμπεται από διάφορα άτομα. Ba Hg Tl 400 500 600 700 nm Ποιο φάσμα χαρακτηρίζεται ως γραμμικό; Σχισμή Πρίσμα Φωτεινή
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΙΑΓΩΝΙΣΜΑ Α
 ΘΕΜΑ ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΙΑΓΩΝΙΣΜΑ Α Α Ποιο φαινόμενο ονομάζεται διασκεδασμός του φωτός; Πώς εξαρτάται ο δείκτης διάθλασης ενός οπτικού μέσου από το μήκος κύματος; Β Στις παρακάτω ερωτήσεις πολλαπλής
ΘΕΜΑ ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΙΑΓΩΝΙΣΜΑ Α Α Ποιο φαινόμενο ονομάζεται διασκεδασμός του φωτός; Πώς εξαρτάται ο δείκτης διάθλασης ενός οπτικού μέσου από το μήκος κύματος; Β Στις παρακάτω ερωτήσεις πολλαπλής
ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ
 1 ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1- και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σχετικά µε τις ιδιότητες
1 ΕΠΑ.Λ. Β ΟΜΑ ΑΣ ΦΥΣΙΚΗ I ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1- και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σχετικά µε τις ιδιότητες
ΠΟΣΟ ΜΕΓΑΛΑ ΕΙΝΑΙ ΤΑ ΑΣΤΕΡΙΑ;
 ΠΟΣΟ ΜΕΓΑΛΑ ΕΙΝΑΙ ΤΑ ΑΣΤΕΡΙΑ; Α) Ακτίνα αστέρων (Όγκος). Στον Ήλιο, και τον Betelgeuse, μπορούμε να μετρήσουμε απευθείας τη γωνιακή διαμέτρο, α, των αστεριών. Αν γνωρίζουμε αυτή τη γωνία, τότε: R ( ακτίνα
ΠΟΣΟ ΜΕΓΑΛΑ ΕΙΝΑΙ ΤΑ ΑΣΤΕΡΙΑ; Α) Ακτίνα αστέρων (Όγκος). Στον Ήλιο, και τον Betelgeuse, μπορούμε να μετρήσουμε απευθείας τη γωνιακή διαμέτρο, α, των αστεριών. Αν γνωρίζουμε αυτή τη γωνία, τότε: R ( ακτίνα
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 25 ΜΑΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 25 ΜΑΙΟΥ 2006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
10. Το ορατό φως έχει μήκη κύματος στο κενό που κυμαίνονται περίπου από: α nm β. 400nm - 600nm γ. 400nm - 700nm δ. 700nm nm.
 ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
ΚΕΦΑΛΑΙΟ 1 ΤΟ ΦΩΣ ΓΡΗΓΟΡΗ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑ - ΑΣΚΗΣΕΙΣ 1. Με τον όρο ότι το φως έχει διπλή φύση εννοούμε ότι: α. είναι εγκάρσιο κύμα. β. αποτελείται από μικρά σωματίδια. γ. συμπεριφέρεται σαν κύμα και σαν
ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ ΑΠΟΡΡΟΦΗΣΗΣ
 ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες Τα άτομα και μόρια, βρίσκονται σε διακριτές ενεργειακές στάθμες και Υφίστανται μεταβάσεις μεταξύ αυτών των ενεργειακών σταθμών όταν αλληλεπιδρούν
ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες Τα άτομα και μόρια, βρίσκονται σε διακριτές ενεργειακές στάθμες και Υφίστανται μεταβάσεις μεταξύ αυτών των ενεργειακών σταθμών όταν αλληλεπιδρούν
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την ηλεκτροµαγνητική θεωρία
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 Στις ερωτήσεις 1-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε την ηλεκτροµαγνητική θεωρία
Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ
 Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
d = 10(m-M+5)/5 pc. (m-m distance modulus)
 Παρατηρησιακά χαρακτηριστικά αστέρων Α. Πόσο μακρυά βρίσκονται τα αστέρια; Μέση απόσταση Γης-'Ηλιου=1AU=149597870,7 km Απόσταση αστέρα: 206264 d= AU ή p'' d= 1 pc, p' ' όπου p είναι η παράλλαξη του αστέρα
Παρατηρησιακά χαρακτηριστικά αστέρων Α. Πόσο μακρυά βρίσκονται τα αστέρια; Μέση απόσταση Γης-'Ηλιου=1AU=149597870,7 km Απόσταση αστέρα: 206264 d= AU ή p'' d= 1 pc, p' ' όπου p είναι η παράλλαξη του αστέρα
Το ατομικό πρότυπο του Βohr μπορεί να περιγράψει το γραμμικό φάσμα των στοιχείων α. Α και Β β. Β και Γ γ. μόνο του Α δ. μόνο του Β.
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 01 ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ 01 ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά
Το φως ταξιδεύει γρηγορότερα από τον ήχο. Γι αυτό μερικοί άνθρωποι φαίνονται λαμπεροί μέχρι να αρχίσουν να μιλάνε.
 Άσκηση 6 Μελέτη φασμάτων Το φως ταξιδεύει γρηγορότερα από τον ήχο. Γι αυτό μερικοί άνθρωποι φαίνονται λαμπεροί μέχρι να αρχίσουν να μιλάνε. ΑΝΤΙΚΕΙΜΕΝΟ ΜΕΛΕΤΗΣ Η βαθμολογία φασματοσκοπίου και η μελέτη
Άσκηση 6 Μελέτη φασμάτων Το φως ταξιδεύει γρηγορότερα από τον ήχο. Γι αυτό μερικοί άνθρωποι φαίνονται λαμπεροί μέχρι να αρχίσουν να μιλάνε. ΑΝΤΙΚΕΙΜΕΝΟ ΜΕΛΕΤΗΣ Η βαθμολογία φασματοσκοπίου και η μελέτη
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2012
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 01 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 01 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία
ΑΠΑΝΤΗΣΕΙΣ. Επιµέλεια: Οµάδα Φυσικών της Ώθησης
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Φυσικών της Ώθησης ΘΕΜΑ A ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Παρασκευή, 0 Μαΐου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΦΥΣΙΚΗ Στις ερωτήσεις Α -Α να γράψετε στο τετράδιό σας τον
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Φυσικών της Ώθησης ΘΕΜΑ A ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Παρασκευή, 0 Μαΐου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΦΥΣΙΚΗ Στις ερωτήσεις Α -Α να γράψετε στο τετράδιό σας τον
Μονάδες Το γραμμικό φάσμα του ατόμου του υδρογόνου ερμηνεύεται με
 Προτεινόµενα Θέµατα Γ Λυκείου Οκτώβριος 20 Φυσική ΘΕΜΑ A γενιικής παιιδείίας Στις ερωτήσεις -5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Η υπεριώδης ακτινοβολία
Προτεινόµενα Θέµατα Γ Λυκείου Οκτώβριος 20 Φυσική ΘΕΜΑ A γενιικής παιιδείίας Στις ερωτήσεις -5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Η υπεριώδης ακτινοβολία
ΦΑΣΜΑ ΕΚΠΟΜΠΗΣ ΛΑΜΠΤΗΡΑ ΠΥΡΑΚΤΩΣΕΩΣ
 1 ΕΚΦΕ Ν.ΚΙΛΚΙΣ 1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΑΝΑΛΥΣΗ ΦΩΤΟΣ ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ ΚΑΙ ΑΠΟΡΡΟΦΗΣΗΣ ΥΠΟΛΟΓΙΣΜΟΣ
1 ΕΚΦΕ Ν.ΚΙΛΚΙΣ 1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΠΕΞΕΡΓΑΣΙΑ : Κ. ΚΟΥΚΟΥΛΑΣ, ΦΥΣΙΚΟΣ - ΡΑΔΙΟΗΛΕΚΤΡΟΛΟΓΟΣ [ Ε.Λ. ΠΟΛΥΚΑΣΤΡΟΥ ] ΑΝΑΛΥΣΗ ΦΩΤΟΣ ΦΑΣΜΑΤΑ ΕΚΠΟΜΠΗΣ ΚΑΙ ΑΠΟΡΡΟΦΗΣΗΣ ΥΠΟΛΟΓΙΣΜΟΣ
Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015
 Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΜΟΝΟ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΜΟΝΟ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα
ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες ΕΦΑΡΜΟΓΗ ΣΤΑ ΦΑΣΜΑΤΑ
 ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες ΕΦΑΡΜΟΓΗ ΣΤΑ ΦΑΣΜΑΤΑ Ένα σημαντικό αποτέλεσμα της κβαντομηχανικής θεωρίας είναι ότι τα μόρια, όχι μόνο βρίσκονται σε διακριτές ενεργειακές
ΚΒΑΝΤΙΚΗ ΦΥΣΙΚΗ: Τα άτομα έχουν διακριτές ενεργειακές στάθμες ΕΦΑΡΜΟΓΗ ΣΤΑ ΦΑΣΜΑΤΑ Ένα σημαντικό αποτέλεσμα της κβαντομηχανικής θεωρίας είναι ότι τα μόρια, όχι μόνο βρίσκονται σε διακριτές ενεργειακές
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα, το γράμμα που αντιστοιχεί στη σωστή φράση η οποία συμπληρώνει σωστά την ημιτελή
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και, δίπλα, το γράμμα που αντιστοιχεί στη σωστή φράση η οποία συμπληρώνει σωστά την ημιτελή
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΞΙΣΩΣΗ Η/Μ ΚΥΜΑΤΟΣ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΞΙΣΩΣΗ Η/Μ ΚΥΜΑΤΟΣ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
 ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας
ΑΡΧΗ ΜΗΝΥΜΑΤΟΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο ΤΕΤΑΡΤΗ 14 ΙΟΥΝΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό κάθε μίας από τις παρακάτω ερωτήσεις Α.1- Α.4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 2011-2012 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό κάθε μίας από τις παρακάτω ερωτήσεις Α.1- Α.4 και δίπλα το
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 2011-2012 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό κάθε μίας από τις παρακάτω ερωτήσεις Α.1- Α.4 και δίπλα το
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 MAΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 8 MAΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 8 MAΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ
 ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ Α] Τα ηλεκτρομαγνητικά κύματα Τι είναι τα ηλεκτρομαγνητικά κύματα Πρόκειται για μια σύνθεση που μπορεί να περιγραφεί με όρους ηλεκτρικού και μαγνητικού πεδίου. Πράγματι τα διανύσματα
ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ ΤΟ ΦΩΣ Α] Τα ηλεκτρομαγνητικά κύματα Τι είναι τα ηλεκτρομαγνητικά κύματα Πρόκειται για μια σύνθεση που μπορεί να περιγραφεί με όρους ηλεκτρικού και μαγνητικού πεδίου. Πράγματι τα διανύσματα
αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό
 αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό Αστερισμός του χαμαιλέοντα Φυσικά χαρακτηριστικά αστέρων Λαμπρότητα Μέγεθος Θερμοκρασία-χρώμα Φασματικός τύπος Λαμπρότητα
αστερισμοί Φαινομενικά αμετάβλητοι σχηματισμοί αστέρων που παρατηρούμε στον ουρανό Αστερισμός του χαμαιλέοντα Φυσικά χαρακτηριστικά αστέρων Λαμπρότητα Μέγεθος Θερμοκρασία-χρώμα Φασματικός τύπος Λαμπρότητα
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 2 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΤΕΛΟΣ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 2 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΠΤΑ (7) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑ 1 ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύμφωνα με την ηλεκτρομαγνητική
ΘΕΜΑ 1 ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση. 1. Σύμφωνα με την ηλεκτρομαγνητική
ΤΡΟΠΟΙ ΔΙΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ Είναι τρείς και σχηματικά φαίνονται στο σχήμα
 ΔΙΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΤΡΟΠΟΙ ΔΙΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ Είναι τρείς και σχηματικά φαίνονται στο σχήμα Μεταφορά Αγωγή Ακτινοβολία Ακτινοβολία ΑΓΩΓΗ (1 ΟΣ ΜΗΧΑΝΙΣΜΟΣ ΜΕΤΑΦΟΡΑΣ ΘΕΡΜΟΤΗΤΑΣ) Έστω δύο σώματα που διατηρούνται
ΔΙΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΤΡΟΠΟΙ ΔΙΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ Είναι τρείς και σχηματικά φαίνονται στο σχήμα Μεταφορά Αγωγή Ακτινοβολία Ακτινοβολία ΑΓΩΓΗ (1 ΟΣ ΜΗΧΑΝΙΣΜΟΣ ΜΕΤΑΦΟΡΑΣ ΘΕΡΜΟΤΗΤΑΣ) Έστω δύο σώματα που διατηρούνται
ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα, που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΜΑΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 5 ΜΑΙΟΥ 6 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 20 ΜΑΪΟΥ 2013 ΕΚΦΩΝΗΣΕΙΣ
 Θέµα Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 013 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία
Θέµα Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΛΥΚΕΙΟΥ & ΕΠΑ.Λ. Β 0 ΜΑΪΟΥ 013 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση, η οποία
The 38 th International Physics Olympiad Iran Theory Competition Sunday, 15 July 2007
 The 38 th International Physics Olympiad Iran Theory Competition Sunday, 5 July 007 Παρακαλώ διαβάστε πρώτα τις πιο κάτω οδηγίες:. Η εξέταση διαρκεί 5 h (πέντε ώρες). Υπάρχουν τρεις ερωτήσεις και κάθε
The 38 th International Physics Olympiad Iran Theory Competition Sunday, 5 July 007 Παρακαλώ διαβάστε πρώτα τις πιο κάτω οδηγίες:. Η εξέταση διαρκεί 5 h (πέντε ώρες). Υπάρχουν τρεις ερωτήσεις και κάθε
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση Η/Μ ΚΥΜΑΤΑ. Ερωτήσεις Πολλαπλής επιλογής
 Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
Η/Μ ΚΥΜΑΤΑ 1. Τα ηλεκτροµαγνητικά κύµατα: Ερωτήσεις Πολλαπλής επιλογής α. είναι διαµήκη. β. υπακούουν στην αρχή της επαλληλίας. γ. διαδίδονται σε όλα τα µέσα µε την ίδια ταχύτητα. δ. Δημιουργούνται από
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α Στις ερωτήσεις Α1-Α4
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α Στις ερωτήσεις Α1-Α4
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 01 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την ηµιτελή
ΘΕΜΑ Α ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 01 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει σωστά την ηµιτελή
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΔΕΥΤΕΡΑ 20 ΜΑΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΔΕΥΤΕΡΑ 0 ΜΑΙΟΥ 013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Θέμα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΔΕΥΤΕΡΑ 0 ΜΑΙΟΥ 013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Θέμα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝ. ΠΑΙΔΕΙΑΣ Γ' ΛΥΚΕΙΟΥ
 05 2 0 ΘΕΡΙΝΑ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝ. ΠΑΙΔΕΙΑΣ Γ' ΛΥΚΕΙΟΥ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση..
05 2 0 ΘΕΡΙΝΑ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΓΕΝ. ΠΑΙΔΕΙΑΣ Γ' ΛΥΚΕΙΟΥ ΘΕΜΑ ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση..
δ. διπλάσιος του αριθµού των νετρονίων του πυρήνα του ατόµου.
 1 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 MAΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα
1 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 MAΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. β. ανιχνεύεται με τους φωρατές υπερύθρου.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΛΙΟΥ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1ο Στις ημιτελείς προτάσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΛΙΟΥ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1ο Στις ημιτελείς προτάσεις
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 20 ΜΑΪΟΥ 2013 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 20 ΜΑΪΟΥ 2013 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 013 - ΕΞΕΤΑΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 013 - ΕΞΕΤΑΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ
Βαθμολογία φασματοσκοπίου και προσδιορισμός φασμάτων εκπομπής και απορρόφησης
 O9 Βαθμολογία φασματοσκοπίου και προσδιορισμός φασμάτων εκπομπής και απορρόφησης 1. Σκοπός Όταν αναλύσουμε το φως που εκπέμπεται από ένα σώμα τότε λαμβάνουμε το φάσμα του. Ειδικά το φάσμα των αερίων αποτελείται
O9 Βαθμολογία φασματοσκοπίου και προσδιορισμός φασμάτων εκπομπής και απορρόφησης 1. Σκοπός Όταν αναλύσουμε το φως που εκπέμπεται από ένα σώμα τότε λαμβάνουμε το φάσμα του. Ειδικά το φάσμα των αερίων αποτελείται
ΑΚΤΙΝΟΒΟΛΙΑ. Εκπέμπεται από σώματα που έχουν θερμοκρασία Τ > 0 Κ. Χαρακτηρίζεται από το μήκος κύματος η τη συχνότητα
 ΑΚΤΙΝΟΒΟΛΙΑ Μεταφορά ενέργειας (με φωτόνια ή ηλεκτρομαγνητικά κύματα) Εκπέμπεται από σώματα που έχουν θερμοκρασία Τ > 0 Κ Χαρακτηρίζεται από το μήκος κύματος η τη συχνότητα Φασματικές περιοχές στο σύστημα
ΑΚΤΙΝΟΒΟΛΙΑ Μεταφορά ενέργειας (με φωτόνια ή ηλεκτρομαγνητικά κύματα) Εκπέμπεται από σώματα που έχουν θερμοκρασία Τ > 0 Κ Χαρακτηρίζεται από το μήκος κύματος η τη συχνότητα Φασματικές περιοχές στο σύστημα
Κεφάλαιο 6 ο : Φύση και
 Κεφάλαιο 6 ο : Φύση και Διάδοση του Φωτός Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Η εξέλιξη ξ των αντιλήψεων για την όραση Ορισμένοι αρχαίοι Έλληνες φιλόσοφοι ερμήνευαν την
Κεφάλαιο 6 ο : Φύση και Διάδοση του Φωτός Φυσική Γ Γυμνασίου Βασίλης Γαργανουράκης http://users.sch.gr/vgargan Η εξέλιξη ξ των αντιλήψεων για την όραση Ορισμένοι αρχαίοι Έλληνες φιλόσοφοι ερμήνευαν την
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε στο τετράδιό σας τον αριθμό της αρχικής
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 24 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο Στις προτάσεις 1.1-1.4 να γράψετε στο τετράδιό σας τον αριθμό της αρχικής
δ. εξαρτάται µόνο από το υλικό του οπτικού µέσου. Μονάδες 4
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 7 ΙΟΥΛΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Κατά την ανάλυση λευκού φωτός από
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Κατά την ανάλυση λευκού φωτός από
ΑΓ.ΚΩΝΣΤΑΝΤΙΝΟΥ ΠΕΙΡΑΙΑΣ ΤΗΛ , ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ. Φως
 ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Κεφάλαιο 1 ο Φως Ο μαθητής που έχει μελετήσει το κεφάλαιο του φωτός πρέπει: Να γνωρίζει πως εξελίχθηκε ιστορικά η έννοια του φωτός και ποια είναι η σημερινή
ΟΔΗΓΙΕΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Κεφάλαιο 1 ο Φως Ο μαθητής που έχει μελετήσει το κεφάλαιο του φωτός πρέπει: Να γνωρίζει πως εξελίχθηκε ιστορικά η έννοια του φωτός και ποια είναι η σημερινή
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α Στις ερωτήσεις Α1-Α4
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Δ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Θέμα Α Στις ερωτήσεις Α1-Α4
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 23 MAΪΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1-Α3 να
Α3. Σε κύκλωμα LC που εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις η ολική ενέργεια είναι α. ανάλογη του φορτίου του πυκνωτή
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΠΑΡΑΣΚΕΥΗ 25 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α Στις ημιτελείς
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΠΑΡΑΣΚΕΥΗ 25 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α Στις ημιτελείς
Γ ΚΥΚΛΟΣ ΣΥΓΧΡΟΝΩΝ ΠΡΟΣΟΜΟΙΩΤΙΚΩΝ ΔΙΑΓΩΝΙΣΜΑΤΩΝ Προτεινόμενα Θέματα Γ ΓΕΛ Φεβρουάριος Φυσική ΘΕΜΑ Α
 Φυσική ΘΕΜΑ Α γενικής παιδείας Να γράψετε τον αριθμό καθεμιάς από τις παρακάτω προτάσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σύμφωνα με το πρότυπο του Bohr για το άτομο του
Φυσική ΘΕΜΑ Α γενικής παιδείας Να γράψετε τον αριθμό καθεμιάς από τις παρακάτω προτάσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Σύμφωνα με το πρότυπο του Bohr για το άτομο του
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 12 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 12 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 12 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Στις ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΜΟΝΟ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 20 ΜΑΪΟΥ 2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΜΟΝΟ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 20 ΜΑΪΟΥ 2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
